Question

Mass 2m is kept on a smooth circular track of mass m which is kept on a smooth horizontal surface. The circular track is given a horizontal velocity $\sqrt{2gR}$ towards left and released. Find the maximum height reached by 2m.

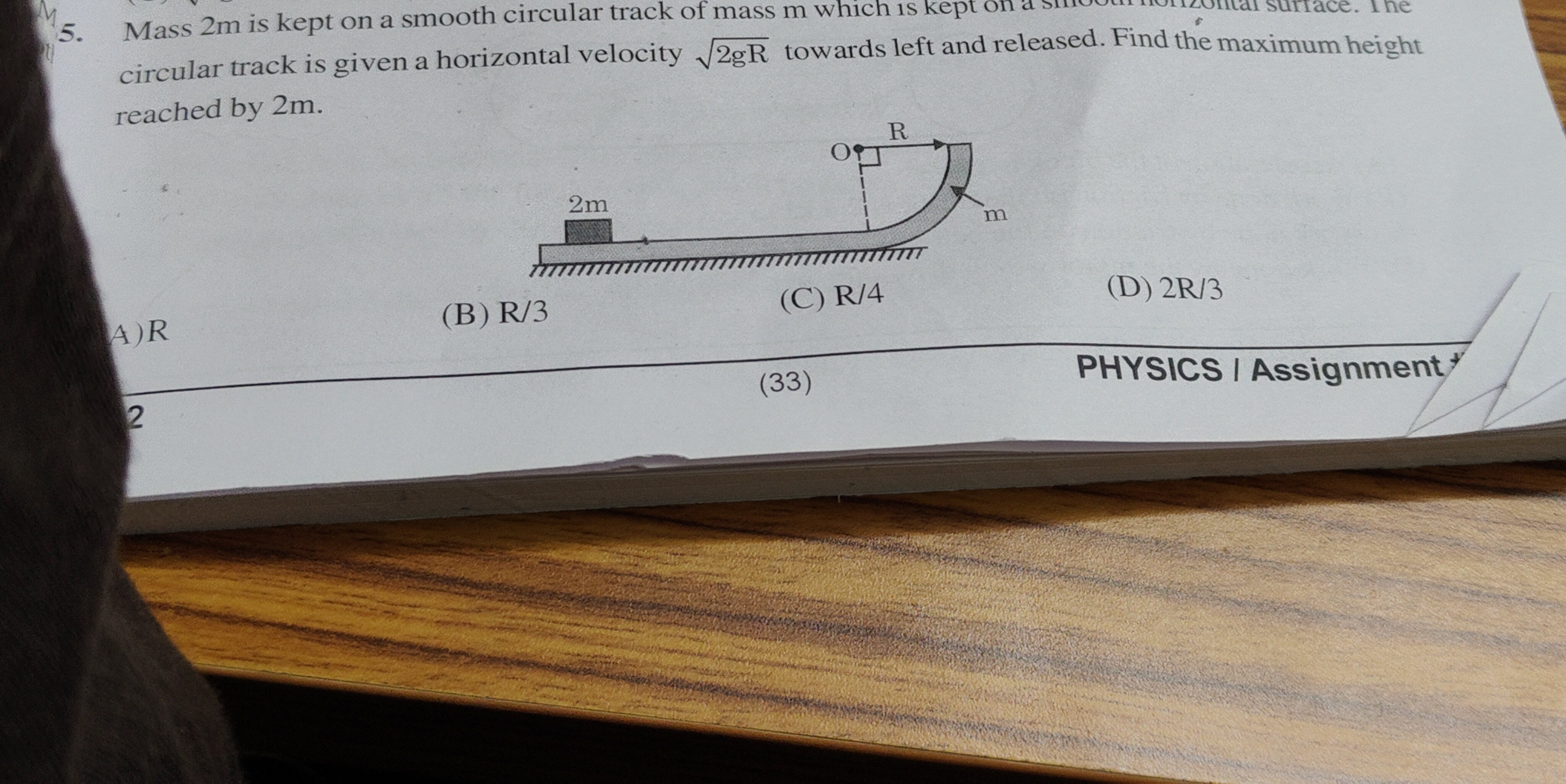
• A. R
• B. R/3
• C. R/4
• D. 2R/3

Answer 1

Answer: (B)

R/3

Answer 2

The problem describes a system consisting of a block of mass 2m on a smooth circular track of mass m. The track itself is on a smooth horizontal surface. We are asked to find the maximum height reached by the block 2m when the track is given an initial horizontal velocity.

1. Analyze the System and Initial Conditions:

• System: The block (mass 2m) and the track (mass m).

• External Forces: Gravity and normal force from the horizontal surface. Since the horizontal surface is smooth, there are no external horizontal forces acting on the system.

• Internal Forces: Normal force between the block and the track. Since the track is smooth, there is no friction.

• Conservation Laws:

  • Since there are no external horizontal forces, the total horizontal momentum of the system is conserved.
  • Since all surfaces are smooth (no friction) and gravity is a conservative force, the total mechanical energy of the system is conserved.

• Initial State: The problem states: "The circular track is given a horizontal velocity $\sqrt{2gR}$ towards left and released." The diagram shows the block 2m on the flat part of the track, and the curved part (ramp) is to the right. If the track moves left, the block 2m (if initially at rest relative to the ground) would move relatively to the right away from the ramp, or simply be left behind. This contradicts the question asking for the maximum height reached on the ramp. Therefore, we must assume there is a typo in the direction, and the initial velocity is given to the track towards the right, or the diagram should be interpreted differently. A common interpretation for such problems to make physical sense is that the block 2m is initially at rest relative to the ground, and the track m is given the initial velocity U = \sqrt{2gR} towards the right (so the block can climb the ramp).

  Let U = \sqrt{2gR}. Initial velocity of track m: $v_{m,i} = U$ (towards right). Initial velocity of block 2m: $v_{2m,i} = 0$ (initially at rest relative to the ground).

2. Final State (at Maximum Height):

• When the block 2m reaches its maximum height h on the track, its vertical velocity relative to the track becomes zero. At this point, the block and the track will move together with a common horizontal velocity v_f.

3. Apply Conservation of Horizontal Momentum:

• Initial horizontal momentum ($P_i$): $P_i = m \cdot v_{m,i} + 2m \cdot v_{2m,i} = mU + 2m(0) = mU$
• Final horizontal momentum ($P_f$): $P_f = (m + 2m) \cdot v_f = 3m v_f$
• By conservation of momentum: $P_i = P_f$ $mU = 3m v_f$ $v_f = \frac{U}{3}$

4. Apply Conservation of Mechanical Energy:

• Initial Kinetic Energy ($KE_i$): $KE_i = \frac{1}{2} m v_{m,i}^2 + \frac{1}{2} (2m) v_{2m,i}^2 = \frac{1}{2} m U^2 + \frac{1}{2} (2m) (0)^2 = \frac{1}{2} m U^2$
• Initial Potential Energy ($PE_i$): Let's set the initial horizontal surface as the reference level for potential energy. So, $PE_i = 0$.
• Final Kinetic Energy ($KE_f$): $KE_f = \frac{1}{2} (m + 2m) v_f^2 = \frac{1}{2} (3m) \left(\frac{U}{3}\right)^2 = \frac{1}{2} (3m) \frac{U^2}{9} = \frac{1}{6} m U^2$
• Final Potential Energy ($PE_f$): The block 2m reaches a height h. $PE_f = 2mgh$
• By conservation of mechanical energy: $KE_i + PE_i = KE_f + PE_f$ $\frac{1}{2} m U^2 + 0 = \frac{1}{6} m U^2 + 2mgh$

5. Solve for h:

• $\frac{1}{2} m U^2 - \frac{1}{6} m U^2 = 2mgh$
• $\left(\frac{3}{6} - \frac{1}{6}\right) m U^2 = 2mgh$
• $\frac{2}{6} m U^2 = 2mgh$
• $\frac{1}{3} m U^2 = 2mgh$
• Substitute $U = \sqrt{2gR}$, so $U^2 = 2gR$: $\frac{1}{3} m (2gR) = 2mgh$
• $\frac{2mgR}{3} = 2mgh$
• Divide both sides by $2mg$: $h = \frac{R}{3}$

The maximum height reached by the mass 2m is $R/3$.

The final answer is $\boxed{\text{R/3}}$.

Explanation of the solution:

The problem involves a system where horizontal momentum is conserved due to the absence of external horizontal forces. Mechanical energy is also conserved as surfaces are smooth and gravity is a conservative force.

1. Assume the track is given initial velocity $U = \sqrt{2gR}$ towards the right (to allow the block to climb the ramp, correcting the "towards left" typo). The block starts at rest.
2. At maximum height, the block and track move together with a common horizontal velocity $v_f$.
3. Apply conservation of horizontal momentum: $mU = (m+2m)v_f \implies v_f = U/3$.
4. Apply conservation of mechanical energy: Initial kinetic energy of the track ($1/2 m U^2$) is converted into final kinetic energy of the combined system ($1/2 (3m) v_f^2$) plus the potential energy gained by the block ($2mgh$).
5. Substitute $v_f = U/3$ and $U^2 = 2gR$ into the energy conservation equation to solve for $h$. $1/2 m U^2 = 1/6 m U^2 + 2mgh$ $1/2 m U^2 = 1/6 m U^2 + 2mgh$ $1/3 m U^2 = 2mgh$ $1/3 m (2gR) = 2mgh$ $h = R/3$.

Answer:

The maximum height reached by 2m is R/3. The correct option is (B).