Question
Question: Let $P = \frac{5}{\frac{1}{\log_2 x} + \frac{1}{\log_3 x} + \frac{1}{\log_4 x} + \frac{1}{\log_5 x}}...
Let P=log2x1+log3x1+log4x1+log5x15 and (120)P=32, then the value of x be:
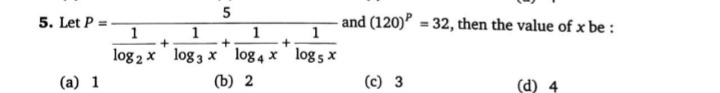
1
2
3
4
2
Solution
The problem requires simplifying a logarithmic expression for P and then using an exponential equation to find the value of x.
1. Simplify the expression for P: The given expression for P is: P=log2x1+log3x1+log4x1+log5x15 Using the change of base formula for logarithms, logba1=logab, we can rewrite each term in the denominator: log2x1=logx2 log3x1=logx3 log4x1=logx4 log5x1=logx5 Substitute these back into the expression for P: P=logx2+logx3+logx4+logx55 Now, use the product rule for logarithms, logaM+logaN=loga(MN): P=logx(2×3×4×5)5 Calculate the product in the argument: 2×3×4×5=6×20=120. So, the expression for P becomes: P=logx1205 Apply the change of base formula again, logba1=logab: P=5log120x
2. Solve the given equation for P: The given equation is (120)P=32. To solve for P, take the logarithm with base 120 on both sides of the equation: log120((120)P)=log12032 Using the power rule for logarithms, logb(Mn)=nlogbM, and the property logbb=1: Plog120120=log12032 P×1=log12032 P=log12032
3. Equate the two expressions for P and solve for x: We have two expressions for P: From step 1: P=5log120x From step 2: P=log12032 Equating them: 5log120x=log12032 Apply the power rule for logarithms to the left side: log120(x5)=log12032 Since the bases of the logarithms are the same, their arguments must be equal: x5=32 We know that 25=32. Therefore, x=2.
4. Check domain restrictions: For the original logarithmic terms logbx to be defined, x must be greater than 0 (x>0). Also, for the terms logbx1 to be defined, logbx cannot be zero, which means x=1. Our solution x=2 satisfies both conditions (2>0 and 2=1).
