Question

Let $I = \int \frac{3x}{1+2x^4} dx$

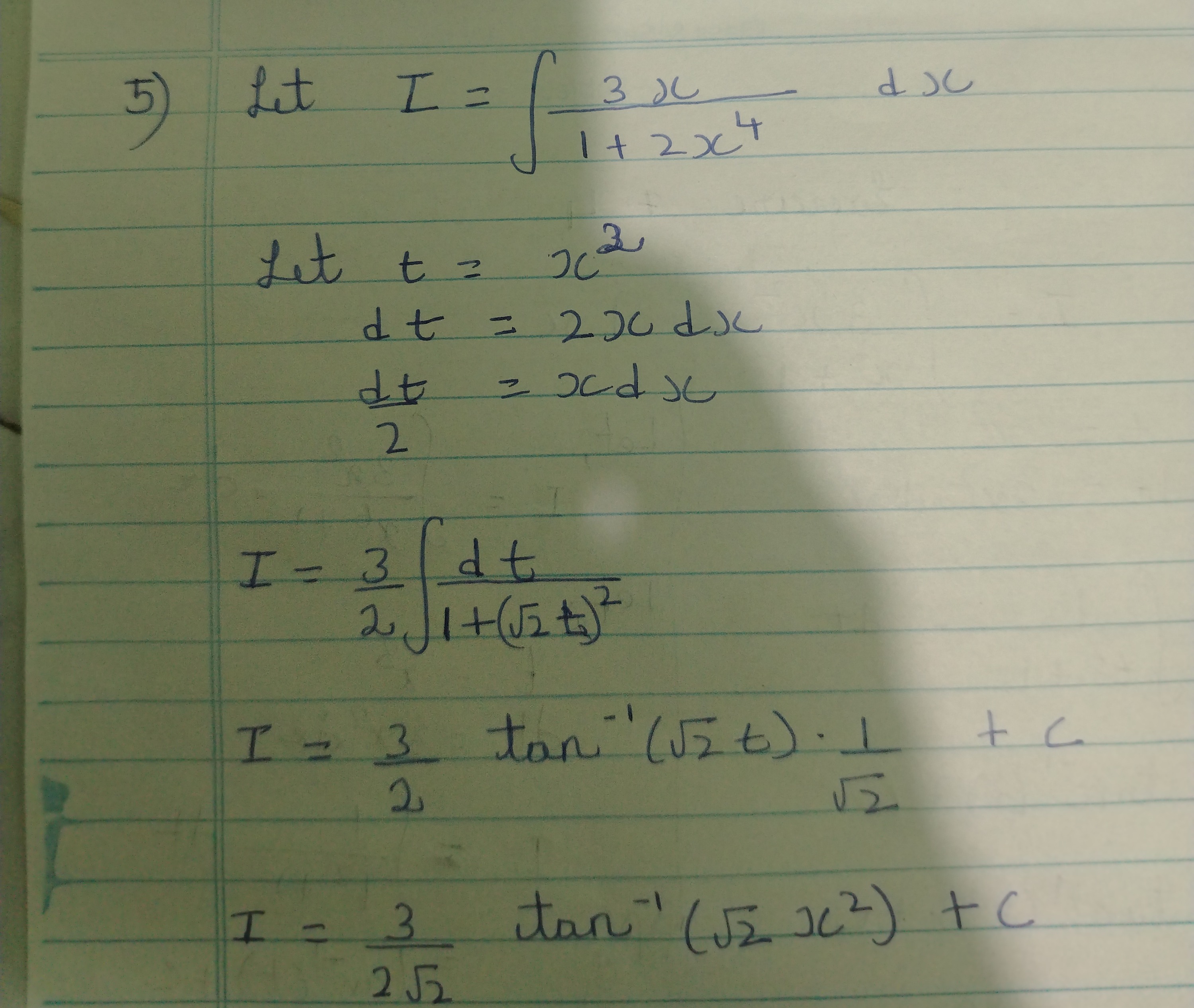
• A. The question asks to solve the indefinite integral $I = \int \frac{3x}{1+2x^4} dx$.
• B. To solve this integral, we use the method of substitution. Notice that the term $x^4$ can be written as $(x^2)^2$, and the numerator contains $x$. This suggests substituting $t = x^2$.
• C. Let $t = x^2$. Then $dt = 2x \, dx$, so $x \, dx = \frac{dt}{2}$. The integral becomes $I = \frac{3}{2} \int \frac{dt}{1+2t^2}$.
• D. The integral is $I = \frac{3}{2\sqrt{2}} \tan^{-1}(\sqrt{2}x^2) + C$.

Answer 1

Answer: (D)

$\frac{3}{2\sqrt{2}} \tan^{-1}(\sqrt{2}x^2) + C$

Answer 2

To solve the indefinite integral $I = \int \frac{3x}{1+2x^4} dx$, we use the substitution method. Let $t = x^2$. Differentiating with respect to $x$, we get $\frac{dt}{dx} = 2x$, which implies $dt = 2x \, dx$, or $x \, dx = \frac{dt}{2}$.

The integral can be rewritten in terms of $t$ as:

$$I = \int \frac{3}{1+2(x^2)^2} (x \, dx) = 3 \int \frac{1}{1+2t^2} \left(\frac{dt}{2}\right) = \frac{3}{2} \int \frac{dt}{1+2t^2}$$

To apply the standard integral formula $\int \frac{1}{a^2+u^2} du = \frac{1}{a} \tan^{-1}\left(\frac{u}{a}\right) + C$, we rewrite the denominator $1+2t^2$ as $1^2 + (\sqrt{2}t)^2$. Let $u = \sqrt{2}t$. Then $du = \sqrt{2} dt$, which means $dt = \frac{du}{\sqrt{2}}$.

Substituting these into the integral:

$$I = \frac{3}{2} \int \frac{1}{1^2 + u^2} \left(\frac{du}{\sqrt{2}}\right) = \frac{3}{2\sqrt{2}} \int \frac{du}{1^2 + u^2}$$

Applying the standard formula with $a=1$:

$$I = \frac{3}{2\sqrt{2}} \left(\frac{1}{1} \tan^{-1}\left(\frac{u}{1}\right)\right) + C = \frac{3}{2\sqrt{2}} \tan^{-1}(u) + C$$

Finally, substitute back $u = \sqrt{2}t$ and $t = x^2$, so $u = \sqrt{2}x^2$:

$$I = \frac{3}{2\sqrt{2}} \tan^{-1}(\sqrt{2}x^2) + C$$

The constant term can be rationalized as $\frac{3\sqrt{2}}{4}$.