Question

Let $f(x) = |(x - 1)| + |(x - 4)| + |(x - 9)| + ..... + |(x - 2401)| + |(x - 2500)| \forall x \in R$. If m and n denote the number of points of non differentiability of $f(x)$ and number of integral points where $f(x)$ has minimum value respectively then

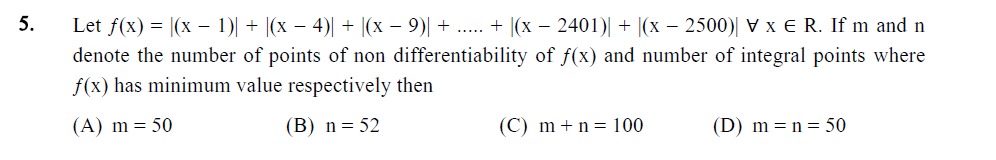
• A. m = 50
• B. n = 52
• C. m + n = 100
• D. m = n = 50

Answer 1

Answer: (A), (B)

A and B

Answer 2

We have

$$f(x)=\sum_{k=1}^{50}|x-k^2|.$$

1. Points of non-differentiability (m):

Each term $|x - k^2|$ is non-differentiable at $x=k^2$. Since the 50 numbers $1^2, 2^2, \dots, 50^2$ are distinct,

$$m=50.$$

2. Integral points where $f(x)$ is minimum (n):

For a sum of absolute values with an even number of terms, the minimum occurs for any $x$ in the interval between the two middle (median) values. Here, the 25th and 26th terms are:

$$25^2=625,\quad 26^2=676.$$

Thus, $f(x)$ is minimum when

$$x\in[625,676].$$

Count of integral points in this interval:

$$n = 676-625+1=52.$$

Conclusion:

• (A) $m=50$ is true.
• (B) $n=52$ is true.
• (C) $m+n=100$ is false (since $50+52=102$).
• (D) $m=n=50$ is false.