Question

Let a, b, c, x, y, z ∈ R such that

$ax + by + cz = 1$

$bx + cy + az = 2$

$cx + ay + bz = 3$.

then the value of $(a³ + b³ + c³ – 3abc)(x³ + y³ + z³ – 3xyz) =$

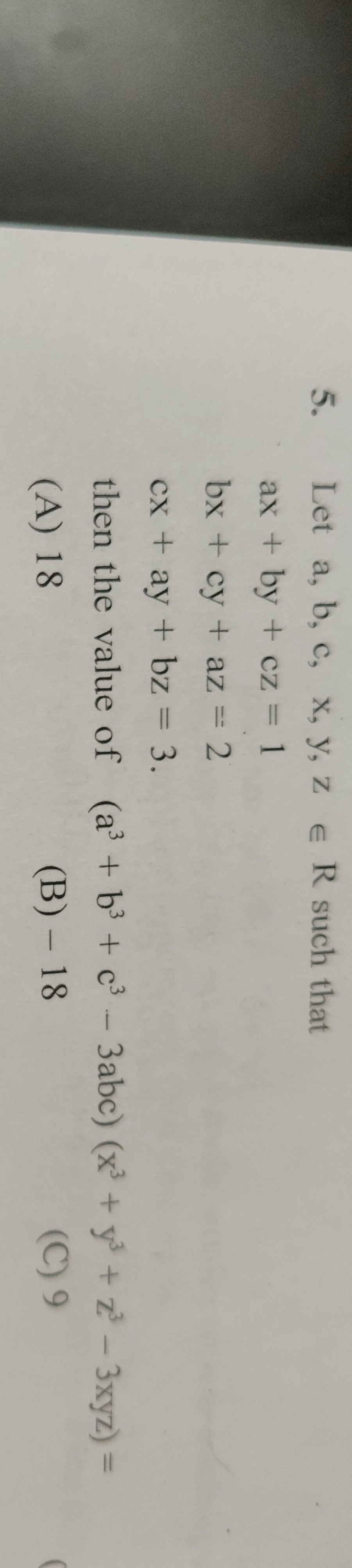
• A. 18
• B. – 18
• C. 9

Answer 1

Answer: (A)

18

Answer 2

The problem asks us to find the value of $(a^3 + b^3 + c^3 – 3abc)(x^3 + y^3 + z^3 – 3xyz)$ given a system of three linear equations.

The given system of equations is:

1. $ax + by + cz = 1$
2. $bx + cy + az = 2$
3. $cx + ay + bz = 3$

We know the algebraic identity:

$A^3 + B^3 + C^3 - 3ABC = (A+B+C)(A+B\omega+C\omega^2)(A+B\omega^2+C\omega)$, where $\omega$ is a complex cube root of unity ($\omega^3=1, 1+\omega+\omega^2=0$).

Let $P_a = a^3 + b^3 + c^3 - 3abc$ and $P_x = x^3 + y^3 + z^3 - 3xyz$.

So, $P_a = (a+b+c)(a+b\omega+c\omega^2)(a+b\omega^2+c\omega)$

And $P_x = (x+y+z)(x+y\omega+z\omega^2)(x+y\omega^2+z\omega)$

We need to find $P_a P_x$.

$P_a P_x = (a+b+c)(x+y+z) \cdot (a+b\omega+c\omega^2)(x+y\omega+z\omega^2) \cdot (a+b\omega^2+c\omega)(x+y\omega^2+z\omega)$

Let's evaluate each product term by term.

Part 1: $(a+b+c)(x+y+z)$

Add the three given equations:

$(ax + by + cz) + (bx + cy + az) + (cx + ay + bz) = 1 + 2 + 3$

$(a+b+c)x + (b+c+a)y + (c+a+b)z = 6$

$(a+b+c)(x+y+z) = 6$

Part 2: $(a+b\omega+c\omega^2)(x+y\omega+z\omega^2)$

Let's expand this product:

$(a+b\omega+c\omega^2)(x+y\omega+z\omega^2)$

$= ax + ay\omega + az\omega^2 + bx\omega + by\omega^2 + bz\omega^3 + cx\omega^2 + cy\omega^3 + cz\omega^4$

Since $\omega^3=1$ and $\omega^4=\omega$:

$= ax + ay\omega + az\omega^2 + bx\omega + by\omega^2 + bz + cx\omega^2 + cy + cz\omega$

Group terms by powers of $\omega$:

$= (ax+bz+cy) + (ay+bx+cz)\omega + (az+by+cx)\omega^2$

Let's compare the coefficients with the given equations:

$ax+by+cz = 1$

$bx+cy+az = 2$

$cx+ay+bz = 3$

The first term is $(ax+cy+bz)$. This is exactly the third equation, $cx+ay+bz = 3$. So, $ax+cy+bz = 3$.

The second term is $(ay+bx+cz)$. This is exactly the first equation, $ax+by+cz = 1$. So, $ay+bx+cz = 1$.

The third term is $(az+by+cx)$. This is exactly the second equation, $bx+cy+az = 2$. So, $az+by+cx = 2$.

Therefore, $(a+b\omega+c\omega^2)(x+y\omega+z\omega^2) = 3 + 1\cdot\omega + 2\cdot\omega^2 = 3+\omega+2\omega^2$.

Part 3: $(a+b\omega^2+c\omega)(x+y\omega^2+z\omega)$

This product is the conjugate of the product in Part 2, assuming $a,b,c,x,y,z$ are real (which is stated in the question).

Let $A_2 = a+b\omega^2+c\omega$ and $X_2 = x+y\omega^2+z\omega$.

$A_2 X_2 = (a+b\omega^2+c\omega)(x+y\omega^2+z\omega)$

$= ax + ay\omega^2 + az\omega + bx\omega^2 + by\omega^4 + bz\omega^3 + cx\omega + cy\omega^3 + cz\omega^2$

Since $\omega^3=1$ and $\omega^4=\omega$:

$= ax + ay\omega^2 + az\omega + bx\omega^2 + by\omega + bz + cx\omega + cy + cz\omega^2$

Group terms by powers of $\omega$:

$= (ax+bz+cy) + (az+by+cx)\omega + (ay+bx+cz)\omega^2$

Using the values from the given equations:

$= 3 + 2\omega + 1\omega^2 = 3+2\omega+\omega^2$.

Now, substitute these parts back into the expression for $P_a P_x$:

$P_a P_x = (6) \cdot (3+\omega+2\omega^2) \cdot (3+2\omega+\omega^2)$

Let's calculate the product of the two complex terms:

$(3+\omega+2\omega^2)(3+2\omega+\omega^2)$

$= 3(3+2\omega+\omega^2) + \omega(3+2\omega+\omega^2) + 2\omega^2(3+2\omega+\omega^2)$

$= (9+6\omega+3\omega^2) + (3\omega+2\omega^2+\omega^3) + (6\omega^2+4\omega^3+2\omega^4)$

Substitute $\omega^3=1$ and $\omega^4=\omega$:

$= (9+6\omega+3\omega^2) + (3\omega+2\omega^2+1) + (6\omega^2+4+2\omega)$

Group terms by powers of $\omega$:

Constant terms: $9+1+4 = 14$

$\omega$ terms: $6\omega+3\omega+2\omega = 11\omega$

$\omega^2$ terms: $3\omega^2+2\omega^2+6\omega^2 = 11\omega^2$

So, the product is $14 + 11\omega + 11\omega^2 = 14 + 11(\omega+\omega^2)$.

Since $1+\omega+\omega^2=0$, we have $\omega+\omega^2 = -1$.

So, the product is $14 + 11(-1) = 14 - 11 = 3$.

Finally, substitute this back into the expression for $P_a P_x$:

$P_a P_x = 6 \cdot 3 = 18$.

The value of $(a^3 + b^3 + c^3 – 3abc)(x^3 + y^3 + z^3 – 3xyz) = 18$.