Question
Question: $\int \frac{e^{4\log x}-e^{5\log x}}{x^5}dx$...
∫x5e4logx−e5logxdx
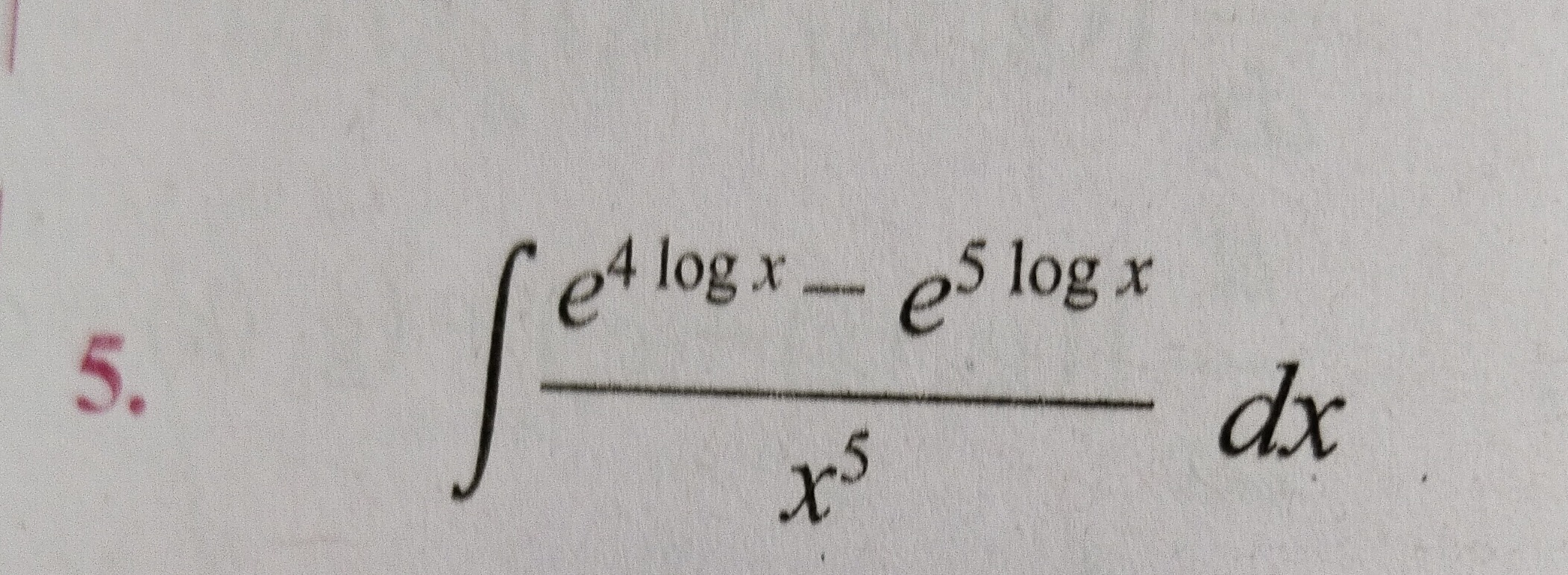
log∣x∣−x+C
Solution
To solve the integral ∫x5e4logx−e5logxdx, we first simplify the terms involving logarithms.
Step 1: Simplify the exponential terms using logarithm properties. Recall the logarithm property: alogb=log(ba). So, e4logx=elog(x4). And e5logx=elog(x5).
Next, recall the property: elogy=y. Using this, we get: elog(x4)=x4 elog(x5)=x5
Step 2: Substitute the simplified terms back into the integral. The integral becomes: ∫x5x4−x5dx
Step 3: Simplify the integrand. Divide each term in the numerator by the denominator: x5x4−x5=x5x4−x5x5=x1−1
Step 4: Integrate the simplified expression. Now, the integral is: ∫(x1−1)dx Integrate each term separately: ∫x1dx−∫1dx Using the standard integral formulas ∫x1dx=log∣x∣+C and ∫kdx=kx+C: log∣x∣−x+C where C is the constant of integration.
The final answer is log∣x∣−x+C.
Explanation of the solution: The problem involves simplifying exponential terms with logarithmic powers using the property ealogx=elogxa=xa. After simplification, the expression becomes a simple rational function which can be split into two terms. Each term is then integrated using standard integration formulas: ∫x1dx=log∣x∣ and ∫1dx=x.
