Question

$\int \frac{e^{4 \log x} - e^{5 \log x}}{x^5} dx$

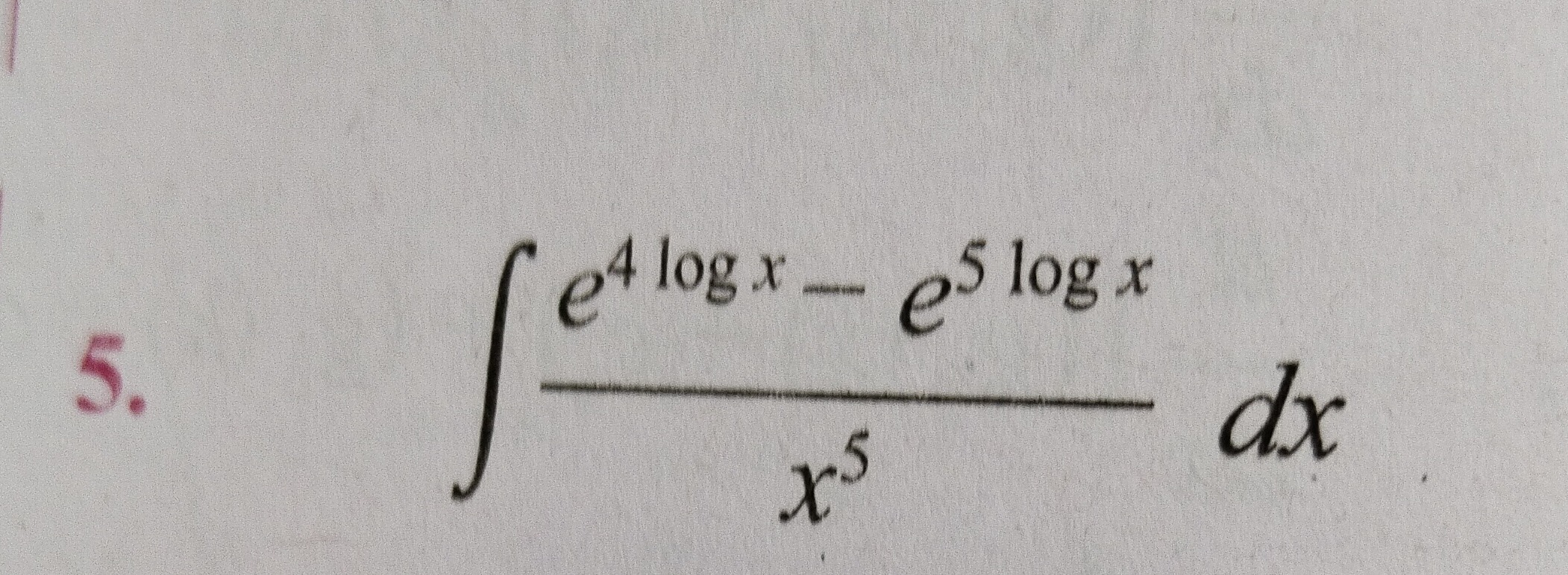
Answer 1

$\log |x| - x + C$

Answer 2

The problem asks us to evaluate the integral $\int \frac{e^{4 \log x} - e^{5 \log x}}{x^5} dx$.

First, we simplify the terms in the numerator using the logarithm property $a \log b = \log b^a$ and the exponential property $e^{\log y} = y$.

1. Simplify $e^{4 \log x}$: $e^{4 \log x} = e^{\log x^4} = x^4$

2. Simplify $e^{5 \log x}$: $e^{5 \log x} = e^{\log x^5} = x^5$

Now, substitute these simplified expressions back into the integral: $\int \frac{x^4 - x^5}{x^5} dx$

Next, we can split the fraction into two separate terms: $\int \left( \frac{x^4}{x^5} - \frac{x^5}{x^5} \right) dx$

Simplify each term: $\int \left( \frac{1}{x} - 1 \right) dx$

Now, we integrate each term separately using the standard integration formulas: $\int \frac{1}{x} dx = \log |x| + C$ $\int k dx = kx + C$ (where k is a constant)

So, the integral becomes: $\int \frac{1}{x} dx - \int 1 dx = \log |x| - x + C$ where $C$ is the constant of integration.