Question

If the value of the definite integral $\int_{-1}^{1} \cot^{-1}(\frac{1}{\sqrt{1-x^2}})\cdot(\cot^{-1}\frac{x}{\sqrt{1-(x^2)^{|x|}}})dx = \frac{\pi^2 (\sqrt{a} - \sqrt{b})}{\sqrt{c}}$, where $a, b, c \in N$ in their lowest form, then find the value of $(a + b + c)$.

Answer 1

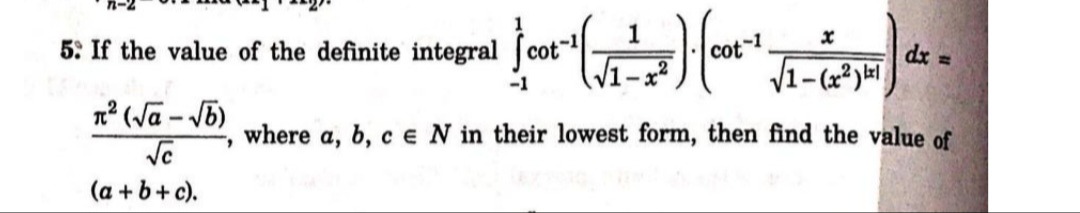
7

Answer 2

Let the integral be $I$. The integrand is $f(x) = \cot^{-1}(\frac{1}{\sqrt{1-x^2}})\cdot(\cot^{-1}\frac{x}{\sqrt{1-(x^2)^{|x|}}})$.

For $x \in (-1, 1)$, $\sqrt{1-x^2} > 0$. So, $\cot^{-1}(\frac{1}{\sqrt{1-x^2}}) = \tan^{-1}(\sqrt{1-x^2})$. Let $A(x) = \tan^{-1}(\sqrt{1-x^2})$. $A(x)$ is an even function.

Let $B(x) = \cot^{-1}\frac{x}{\sqrt{1-(x^2)^{|x|}}}$. We check the parity of $f(x)$: $f(-x) = \cot^{-1}(\frac{1}{\sqrt{1-(-x)^2}})\cdot(\cot^{-1}\frac{-x}{\sqrt{1-((-x)^2)^{|-x|}}})$. Since $(-x)^2 = x^2$ and $|-x| = |x|$, we have: $f(-x) = \cot^{-1}(\frac{1}{\sqrt{1-x^2}})\cdot(\cot^{-1}\frac{-x}{\sqrt{1-(x^2)^{|x|}}})$. $f(-x) = A(x) \cdot \cot^{-1}(- \frac{x}{\sqrt{1-(x^2)^{|x|}}})$. Using $\cot^{-1}(-y) = \pi - \cot^{-1}(y)$ for $y>0$: $f(-x) = A(x) (\pi - \cot^{-1}\frac{x}{\sqrt{1-(x^2)^{|x|}}})$. $f(-x) = \pi A(x) - A(x) B(x) = \pi A(x) - f(x)$. So, $f(x) + f(-x) = \pi A(x)$.

Using the property $\int_{-a}^{a} f(x) dx = \int_{0}^{a} (f(x) + f(-x)) dx$: $I = \int_{-1}^{1} f(x) dx = \int_{0}^{1} (f(x) + f(-x)) dx = \int_{0}^{1} \pi A(x) dx$. $I = \pi \int_{0}^{1} \tan^{-1}(\sqrt{1-x^2}) dx$.

Let $J = \int_{0}^{1} \tan^{-1}(\sqrt{1-x^2}) dx$. Substitute $x = \cos \theta$, $dx = -\sin \theta d\theta$. When $x=0$, $\theta = \pi/2$. When $x=1$, $\theta = 0$. $J = \int_{\pi/2}^{0} \tan^{-1}(\sin \theta) (-\sin \theta) d\theta = \int_{0}^{\pi/2} \tan^{-1}(\sin \theta) \sin \theta d\theta$. Using integration by parts: $u = \tan^{-1}(\sin \theta)$, $dv = \sin \theta d\theta$. $du = \frac{\cos \theta}{1+\sin^2 \theta} d\theta$, $v = -\cos \theta$. $J = [-\cos \theta \tan^{-1}(\sin \theta)]_{0}^{\pi/2} - \int_{0}^{\pi/2} (-\cos \theta) \frac{\cos \theta}{1+\sin^2 \theta} d\theta$. The boundary term is 0. $J = \int_{0}^{\pi/2} \frac{\cos^2 \theta}{1+\sin^2 \theta} d\theta = \int_{0}^{\pi/2} \frac{1-\sin^2 \theta}{1+\sin^2 \theta} d\theta$. $J = \int_{0}^{\pi/2} \frac{2 - (1+\sin^2 \theta)}{1+\sin^2 \theta} d\theta = \int_{0}^{\pi/2} (\frac{2}{1+\sin^2 \theta} - 1) d\theta$. $J = 2 \int_{0}^{\pi/2} \frac{1}{1+\sin^2 \theta} d\theta - \frac{\pi}{2}$. The integral $\int_{0}^{\pi/2} \frac{1}{1+\sin^2 \theta} d\theta = \int_{0}^{\pi/2} \frac{\sec^2 \theta}{\sec^2 \theta + \tan^2 \theta} d\theta = \int_{0}^{\pi/2} \frac{\sec^2 \theta}{1+2\tan^2 \theta} d\theta$. Let $t = \tan \theta$, $dt = \sec^2 \theta d\theta$. $\int_{0}^{\infty} \frac{dt}{1+2t^2} = \frac{1}{\sqrt{2}} [\tan^{-1}(\sqrt{2}t)]_{0}^{\infty} = \frac{1}{\sqrt{2}} (\frac{\pi}{2} - 0) = \frac{\pi}{2\sqrt{2}}$. So, $J = 2 \cdot \frac{\pi}{2\sqrt{2}} - \frac{\pi}{2} = \frac{\pi}{\sqrt{2}} - \frac{\pi}{2} = \frac{\pi(\sqrt{2}-1)}{2}$.

Therefore, $I = \pi J = \pi \cdot \frac{\pi(\sqrt{2}-1)}{2} = \frac{\pi^2(\sqrt{2}-1)}{2}$. Comparing with $\frac{\pi^2 (\sqrt{a} - \sqrt{b})}{\sqrt{c}}$, we have: $\frac{\pi^2(\sqrt{2}-\sqrt{1})}{\sqrt{4}} = \frac{\pi^2 (\sqrt{a} - \sqrt{b})}{\sqrt{c}}$. Thus, $a=2$, $b=1$, $c=4$. $a+b+c = 2+1+4 = 7$.