Question

If the corner points of the feasible solutions are (0, 10), (2, 2), (4, 0), (3, 2), then the point of minimum value of $z = 3x + 2y$ is

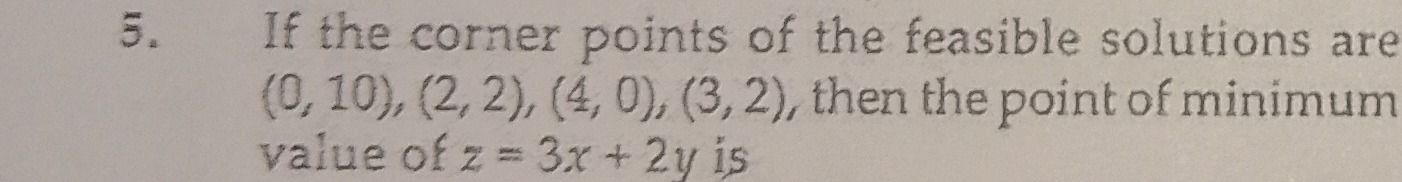
• A. (0, 10)
• B. (2, 2)
• C. (4, 0)
• D. (3, 2)

Answer 1

Answer: (B)

(2, 2)

Answer 2

To find the minimum value of the objective function $z = 3x + 2y$, we evaluate $z$ at each of the given corner points:

• At $(0, 10)$: $z = 3(0) + 2(10) = 0 + 20 = 20$

• At $(2, 2)$: $z = 3(2) + 2(2) = 6 + 4 = 10$

• At $(4, 0)$: $z = 3(4) + 2(0) = 12 + 0 = 12$

• At $(3, 2)$: $z = 3(3) + 2(2) = 9 + 4 = 13$

The minimum value of $z$ is $10$, which occurs at the point $(2, 2)$.