Question
Question: If tan²$\alpha$ + 2tan$\alpha$.tan2$\beta$ = tan²$\beta$ + 2tan$\beta$.tan2$\alpha$, then we may hav...
If tan²α + 2tanα.tan2β = tan²β + 2tanβ.tan2α, then we may have
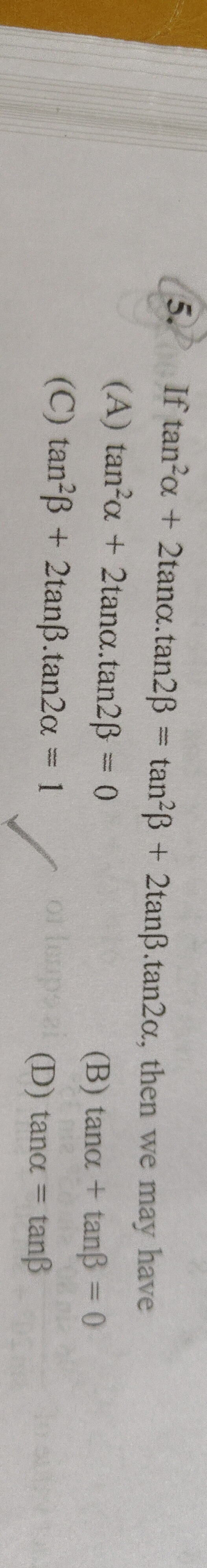
tan²α + 2tanα.tan2β = 0
tanα + tanβ = 0
tan²β + 2tanβ.tan2α = 1
tanα = tanβ
B, D
Solution
The given equation is: tan2α+2tanαtan2β=tan2β+2tanβtan2α
Rearrange the terms: tan2α−tan2β=2tanβtan2α−2tanαtan2β (tanα−tanβ)(tanα+tanβ)=−2(tanαtan2β−tanβtan2α)
Let a=tanα and b=tanβ. The equation becomes: (a−b)(a+b)=−2(atan2β−btan2α)
Now, substitute the double angle formulas: tan2x=1−tan2x2tanx. So, tan2α=1−a22a and tan2β=1−b22b. The equation becomes: (a−b)(a+b)=−2(a1−b22b−b1−a22a) (a−b)(a+b)=−2(1−b22ab−1−a22ab) (a−b)(a+b)=−4ab(1−b21−1−a21) (a−b)(a+b)=−4ab((1−b2)(1−a2)(1−a2)−(1−b2)) (a−b)(a+b)=−4ab((1−a2)(1−b2)b2−a2) (a−b)(a+b)=−4ab((1−a2)(1−b2)−(a2−b2)) (a−b)(a+b)=4ab((1−a2)(1−b2)(a−b)(a+b))
Now, we have two possibilities:
Case 1: (a−b)(a+b)=0 This implies a−b=0 or a+b=0. If a−b=0, then a=b, which means tanα=tanβ. This matches option (D). If a+b=0, then a=−b, which means tanα=−tanβ, or tanα+tanβ=0. This matches option (B).
Case 2: (a−b)(a+b)=0 In this case, we can divide both sides by (a−b)(a+b): 1=(1−a2)(1−b2)4ab (1−a2)(1−b2)=4ab 1−a2−b2+a2b2=4ab 1=a2+b2−a2b2+4ab
Let's check if this third case leads to any of the options. If we substitute tanα=tanβ (from Case 1) into this condition, we get: (1−a2)2=4a2 1−a2=±2a a2±2a−1=0 For a2+2a−1=0, a=2−2±4−4(1)(−1)=−1±2. For a2−2a−1=0, a=22±4−4(1)(−1)=1±2. So, if tanα=tanβ=±1±2, these are specific solutions that also satisfy tanα=tanβ. These values are valid since tanα=±1.
If we substitute tanα=−tanβ (from Case 1) into this condition, we get: Let b=−a. (1−a2)(1−(−a)2)=4a(−a) (1−a2)2=−4a2 (1−a2)2+4a2=0 Since (1−a2)2≥0 and 4a2≥0, their sum can only be zero if both terms are zero. This implies a2=0 and (1−a2)2=0. a=0 from a2=0. Substituting a=0 into (1−a2)2=0 gives (1−0)2=0, which means 1=0. This is a contradiction. The only way for (1−a2)2+4a2=0 to hold is if a is imaginary, which is not possible for real α. However, if a=0, then b=0. In this case, tanα=0 and tanβ=0. This satisfies both tanα=tanβ and tanα+tanβ=0.
So, the general solutions are tanα=tanβ or tanα+tanβ=0. Both options (B) and (D) are derived from the given equation. Since the question asks "then we may have", any of these valid conditions is a correct answer.
