Question

If $\tan \frac{\pi}{24}$ is a root of $x^4 + ax^3 + bx^2 - ax + 1 = 0$ then the value of a + b is (a, b ∈ N)

Answer 1

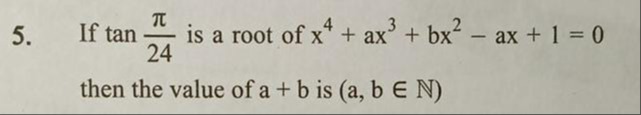
10

Answer 2

The given polynomial equation is $x^4 + ax^3 + bx^2 - ax + 1 = 0$.

Since $x=0$ is not a root (as $1 \neq 0$), we can divide the equation by $x^2$:

$x^2 + ax + b - \frac{a}{x} + \frac{1}{x^2} = 0$

Rearrange the terms:

$\left(x^2 + \frac{1}{x^2}\right) + a\left(x - \frac{1}{x}\right) + b = 0$

Let $y = x - \frac{1}{x}$.

Then, $y^2 = \left(x - \frac{1}{x}\right)^2 = x^2 - 2 + \frac{1}{x^2}$.

So, $x^2 + \frac{1}{x^2} = y^2 + 2$.

Substitute these into the equation:

$(y^2 + 2) + ay + b = 0$

$y^2 + ay + (b+2) = 0$

We are given that $\tan \frac{\pi}{24}$ is a root of the original equation. Let $x = \tan \frac{\pi}{24}$.

Then, $y = \tan \frac{\pi}{24} - \frac{1}{\tan \frac{\pi}{24}} = \tan \frac{\pi}{24} - \cot \frac{\pi}{24}$.

Using the trigonometric identity $\tan \theta - \cot \theta = -2 \cot(2\theta)$:

$y = -2 \cot\left(2 \cdot \frac{\pi}{24}\right) = -2 \cot\left(\frac{\pi}{12}\right)$.

Now, we need to find the value of $\cot\left(\frac{\pi}{12}\right)$.

$\frac{\pi}{12}$ radians is equal to $15^\circ$.

We know that $\tan 15^\circ = \tan(45^\circ - 30^\circ) = \frac{\tan 45^\circ - \tan 30^\circ}{1 + \tan 45^\circ \tan 30^\circ}$.

$\tan 15^\circ = \frac{1 - \frac{1}{\sqrt{3}}}{1 + 1 \cdot \frac{1}{\sqrt{3}}} = \frac{\frac{\sqrt{3}-1}{\sqrt{3}}}{\frac{\sqrt{3}+1}{\sqrt{3}}} = \frac{\sqrt{3}-1}{\sqrt{3}+1}$.

To rationalize the denominator, multiply the numerator and denominator by $(\sqrt{3}-1)$:

$\tan 15^\circ = \frac{(\sqrt{3}-1)(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)} = \frac{(\sqrt{3}-1)^2}{3-1} = \frac{3 - 2\sqrt{3} + 1}{2} = \frac{4 - 2\sqrt{3}}{2} = 2 - \sqrt{3}$.

Then, $\cot 15^\circ = \frac{1}{\tan 15^\circ} = \frac{1}{2 - \sqrt{3}}$.

To rationalize, multiply numerator and denominator by $(2+\sqrt{3})$:

$\cot 15^\circ = \frac{1}{2 - \sqrt{3}} \cdot \frac{2 + \sqrt{3}}{2 + \sqrt{3}} = \frac{2 + \sqrt{3}}{4 - 3} = 2 + \sqrt{3}$.

Substitute this value back into the expression for $y$:

$y = -2(2 + \sqrt{3}) = -4 - 2\sqrt{3}$.

This value of $y$ is a root of the quadratic equation $y^2 + ay + (b+2) = 0$.

Since $a$ and $b$ are natural numbers (and thus rational), the coefficients of this quadratic equation are rational. If one root of a quadratic equation with rational coefficients is $p+q\sqrt{r}$, then its conjugate $p-q\sqrt{r}$ must also be a root.

So, if $y_1 = -4 - 2\sqrt{3}$ is a root, then the other root must be $y_2 = -4 + 2\sqrt{3}$.

Using Vieta's formulas for the sum and product of roots of $y^2 + ay + (b+2) = 0$:

Sum of roots: $y_1 + y_2 = -a$

$(-4 - 2\sqrt{3}) + (-4 + 2\sqrt{3}) = -a$

$-8 = -a \implies a = 8$.

Product of roots: $y_1 y_2 = b+2$

$(-4 - 2\sqrt{3})(-4 + 2\sqrt{3}) = b+2$

This is of the form $(A-B)(A+B) = A^2 - B^2$, where $A=-4$ and $B=2\sqrt{3}$.

$(-4)^2 - (2\sqrt{3})^2 = b+2$

$16 - (4 \cdot 3) = b+2$

$16 - 12 = b+2$

$4 = b+2 \implies b = 2$.

We are given that $a, b \in N$ (natural numbers).

Our calculated values are $a=8$ and $b=2$, which are indeed natural numbers.

Finally, we need to find the value of $a+b$:

$a+b = 8 + 2 = 10$.