Question

If P(x) = ax²+ bx + c, Q(x) = - ax² + dx + c where ac ≠ 0, then P(x).Q(x) = 0 has (where a,b,c,d ∈ R)

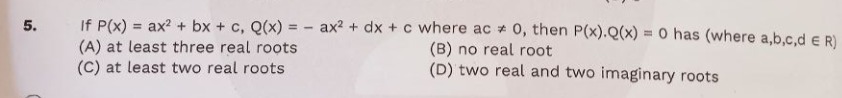
• A. at least three real roots
• B. no real root
• C. at least two real roots
• D. two real and two imaginary roots

Answer 1

Answer: (C)

at least two real roots

Answer 2

We are given

$P(x) = ax^2 + bx + c, \quad Q(x) = -ax^2 + dx + c, \quad \text{with } ac \ne 0.$

The equation $P(x) \cdot Q(x) = 0$ implies that the real roots come from the union of the roots of $P(x) = 0$ and $Q(x) = 0$.

For $P(x) = 0$: The discriminant is $\Delta_P = b^2 - 4ac.$

• If $\Delta_P \ge 0$, $P(x) = 0$ has 2 real roots.
• If $\Delta_P < 0$, $P(x) = 0$ has no real root.

For $Q(x) = 0$: Since $Q(x) = -ax^2 + dx + c$, its discriminant is $\Delta_Q = d^2 - 4 \cdot (-a) \cdot c = d^2 + 4ac.$

• If $\Delta_Q \ge 0$, $Q(x) = 0$ has 2 real roots.
• If $\Delta_Q < 0$, $Q(x) = 0$ has no real root.

Notice that because $ac \ne 0$, the sign of $ac$ plays a role:

1. When $ac > 0$: $\Delta_Q = d^2 + 4ac > 0$ (since $4ac$ is positive) so $Q(x) = 0$ always gives 2 real roots. Even if $P(x) = 0$ has no real root, there are 2 real roots from $Q(x) = 0$.

2. When $ac < 0$: In this case, $P(x) = 0$ always has 2 real roots because $\Delta_P = b^2 - 4ac > b^2$ (since $-4ac > 0$). While $Q(x) = 0$ may or may not have real roots depending on $d$, we already have 2 real roots from $P(x) = 0$.

Thus, in every case, the equation $P(x)Q(x) = 0$ has at least 2 real roots.