Question
Question: If $\int \frac{x(x+1)(2x^2-x+1)}{(x^3+x^2+x-1)^3}dx = \frac{1}{Af^2(x)}+C$ where f(1) = 2 then...
If ∫(x3+x2+x−1)3x(x+1)(2x2−x+1)dx=Af2(x)1+C where f(1) = 2 then
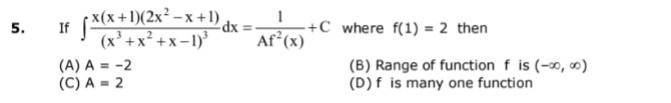
A = -2
Range of function f is (−∞,∞)
A = 2
f is many one function
A = -2, Range of function f is (−∞,∞), f is many one function
Solution
Let the given integral be I.
I=∫(x3+x2+x−1)3x(x+1)(2x2−x+1)dx
We are given that I=Af2(x)1+C. Differentiating the right-hand side with respect to x:
dxd(Af2(x)1)=A1dxd(f(x))−2=A1(−2)(f(x))−3f′(x)=A(f(x))3−2f′(x).
Comparing this with the integrand, we have:
(x3+x2+x−1)3x(x+1)(2x2−x+1)=A(f(x))3−2f′(x).
Let D(x)=x3+x2+x−1. We observe that D(x) can be written as x(x2+x+1−x1).
Let's propose f(x)=x2+x+1−x1. Then D(x)=x⋅f(x).
Substituting this into the comparison equation:
(xf(x))3x(x+1)(2x2−x+1)=A(f(x))3−2f′(x)
x3(f(x))3x(x+1)(2x2−x+1)=A(f(x))3−2f′(x)
x2(x+1)(2x2−x+1)=A−2f′(x)
x3x(x+1)(2x2−x+1)=A−2f′(x).
x2(x+1)(2x2−x+1)=A−2f′(x).
(1+x1)(2−x1+x21)=A−2f′(x).
The left side is 2−x1+x21+x2−x21+x31=2+x1+x31.
Now, let's find f′(x) for f(x)=x2+x+1−x1:
f′(x)=2x+1+x21.
Let's use the relation N(x)=A−2f′(x)(f(x)D(x))3.
If f(x)=x2+x+1−x1, then D(x)=x(x2+x+1−x1)=xf(x).
So f(x)D(x)=x.
Therefore, N(x)=A−2f′(x)x3.
The numerator N(x)=x(x+1)(2x2−x+1)=(x2+x)(2x2−x+1)=2x4−x3+x2+2x3−x2+x=2x4+x3+x.
And f′(x)=dxd(x2+x+1−x1)=2x+1+x21.
So, N(x)=A−2(2x+1+x21)x3=A−2(2x4+x3+x).
Comparing 2x4+x3+x with A−2(2x4+x3+x), we get:
1=A−2⟹A=−2.
So, option (A) is correct.
Now let's verify the condition f(1)=2 and check other options using f(x)=x2+x+1−x1.
-
f(1)=12+1+1−11=1+1+1−1=2. The condition f(1)=2 is satisfied.
-
Option (B): Range of function f is (−∞,∞).
We analyze f(x)=x2+x+1−x1.
The derivative is f′(x)=2x+1+x21.
For x>0: 2x>0, 1>0, x21>0. So f′(x)>0 for all x>0.
Thus f(x) is strictly increasing for x>0.
As x→0+, f(x)→0+0+1−∞=−∞.
As x→∞, f(x)→∞+∞+1−0=∞.
So for x∈(0,∞), the range of f(x) is (−∞,∞).
For x<0: f′(x)=2x+1+x21.
Let's find critical points by setting f′(x)=0: 2x+1+x21=0⟹2x3+x2+1=0.
By inspection, x=−1 is a root: 2(−1)3+(−1)2+1=−2+1+1=0.
So f′(−1)=0.
f(−1)=(−1)2+(−1)+1−(−1)1=1−1+1+1=2.
To determine if x=−1 is a local extremum, we check the sign of f′(x) around x=−1.
f′(x) is a polynomial in terms of x and 1/x2.
As x→−∞, f′(x)→−∞.
As x→0−, f′(x)→∞.
Since f′(−1)=0 and f′(x) goes from −∞ to ∞, x=−1 is a local minimum.
f(−∞)=limx→−∞(x2+x+1−x1)=∞.
f(0−)=limx→0−(x2+x+1−x1)=−∞.
So for x∈(−∞,0), f(x) decreases from ∞ to a minimum of f(−1)=2, and then increases from 2 to −∞.
The range of f(x) for x∈(−∞,0) is (−∞,∞).
Combining both cases, the range of f(x) is (−∞,∞). So option (B) is correct.
- Option (D): f is many one function.
Since f(1)=2 and f(−1)=2, the function takes the same value for different inputs. Therefore, f(x) is a many-one function. So option (D) is correct.
Options (A), (B), and (D) are all correct.
