Question
Question: If $\alpha,\beta$ are two acute angles such that $\alpha + \beta = \gamma$, where $\gamma$ is a cons...
If α,β are two acute angles such that α+β=γ, where γ is a constant, then maximum value of (sinα+cosα+sinβ+cosβ) is
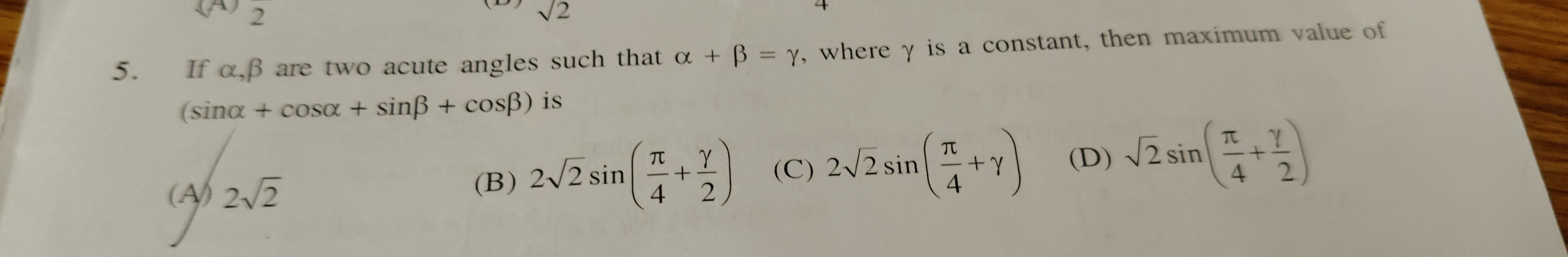
22
22sin(4π+2γ)
22sin(4π+γ)
2sin(4π+2γ)
2\sqrt{2}sin(\frac{\pi}{4}+\frac{\gamma}{2})
Solution
Let the given expression be E.
E=sinα+cosα+sinβ+cosβ
We know the identity asinx+bcosx=a2+b2sin(x+δ), where cosδ=a2+b2a and sinδ=a2+b2b.
For a=1,b=1, we have 12+12=2.
So, sinx+cosx=2(21sinx+21cosx)=2(cos4πsinx+sin4πcosx).
Using the formula sin(A+B)=sinAcosB+cosAsinB, we get:
sinx+cosx=2sin(x+4π).
Applying this to the expression E:
E=2sin(α+4π)+2sin(β+4π)
E=2[sin(α+4π)+sin(β+4π)]
Now, use the sum-to-product trigonometric identity: sinA+sinB=2sin(2A+B)cos(2A−B).
Let A=α+4π and B=β+4π.
Then,
A+B=(α+4π)+(β+4π)=α+β+2π.
Given that α+β=γ, so A+B=γ+2π.
Therefore, 2A+B=2γ+4π.
And,
A−B=(α+4π)−(β+4π)=α−β.
Therefore, 2A−B=2α−β.
Substitute these into the expression for E:
E=2[2sin(2γ+4π)cos(2α−β)]
E=22sin(4π+2γ)cos(2α−β)
To find the maximum value of E, we need to maximize the term cos(2α−β), since 22sin(4π+2γ) is a constant (as γ is a constant).
The maximum value of the cosine function is 1.
So, cos(2α−β) will be maximum when it equals 1.
This occurs when 2α−β=0, which implies α−β=0, or α=β.
Given that α and β are acute angles, 0<α<2π and 0<β<2π.
If α=β, then α+β=2α=γ.
So, α=β=2γ.
For α and β to be acute angles, we must have 0<2γ<2π, which implies 0<γ<π. This condition is consistent with the problem statement.
When cos(2α−β)=1, the maximum value of E is:
Emax=22sin(4π+2γ)×1
Emax=22sin(4π+2γ)
