Question
Question: If all the roots of equation $x^4-(2k+1)x^2+k^2-3k=0$ are real then k can be...
If all the roots of equation x4−(2k+1)x2+k2−3k=0 are real then k can be
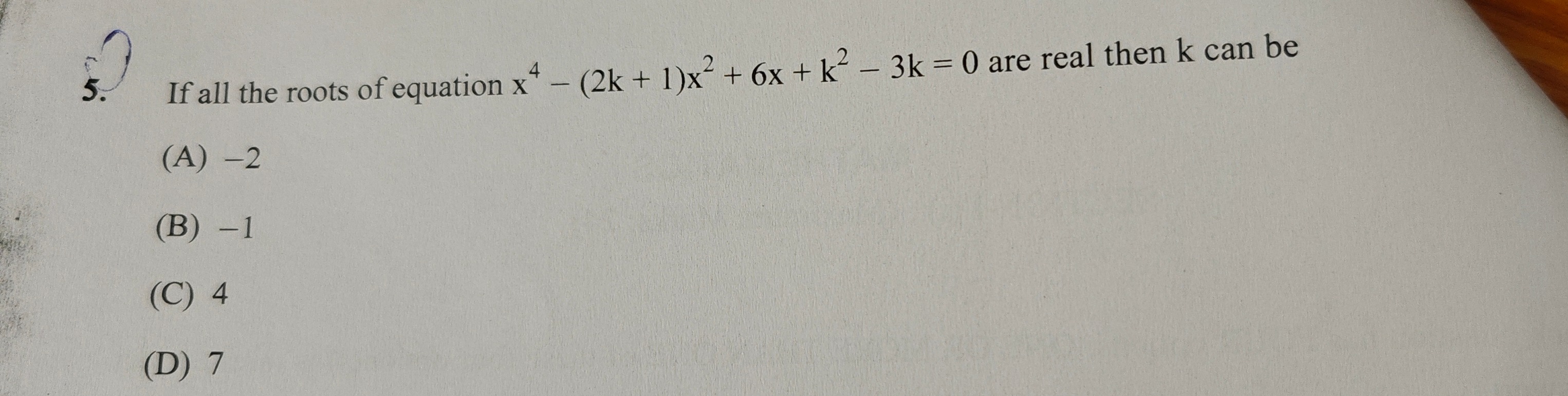
-2
-1
4
7
4, 7
Solution
Let the given equation be x4−(2k+1)x2+k2−3k=0. This is a biquadratic equation. Let y=x2. Substituting y into the equation, we get a quadratic equation in terms of y: y2−(2k+1)y+k2−3k=0.
For all roots of the original equation (x) to be real, x2 must be real and non-negative. This means both roots of the quadratic equation in y (let's call them y1 and y2) must be real and non-negative. For y1,y2≥0, the following conditions must be satisfied:
-
Discriminant (D) must be non-negative (for real roots of y): D=(−(2k+1))2−4(1)(k2−3k) D=(2k+1)2−4(k2−3k) D=(4k2+4k+1)−(4k2−12k) D=4k2+4k+1−4k2+12k D=16k+1 For real roots, D≥0⟹16k+1≥0⟹16k≥−1⟹k≥−161.
-
Sum of roots (y1+y2) must be non-negative: For the quadratic equation ay2+by+c=0, the sum of roots is −b/a. Here, y1+y2=−(−(2k+1))/1=2k+1. For non-negative roots, y1+y2≥0⟹2k+1≥0⟹2k≥−1⟹k≥−21.
-
Product of roots (y1y2) must be non-negative: For the quadratic equation ay2+by+c=0, the product of roots is c/a. Here, y1y2=(k2−3k)/1=k2−3k. For non-negative roots, y1y2≥0⟹k2−3k≥0⟹k(k−3)≥0. This inequality holds when k≤0 or k≥3.
Now, we need to find the values of k that satisfy all three conditions simultaneously:
- Condition 1: k≥−161
- Condition 2: k≥−21
- Condition 3: k∈(−∞,0]∪[3,∞)
Combining Condition 1 and Condition 2: k≥−161 and k≥−21. The stricter of these two is k≥−161.
Intersect k≥−161 with Condition 3 (k≤0 or k≥3):
-
Case 1: k≥−161 AND k≤0. This implies −161≤k≤0.
-
Case 2: k≥−161 AND k≥3. This implies k≥3.
Combining these two cases, the set of all possible values for k is [−161,0]∪[3,∞).
Check the given options against this range: (A) -2: Not in the range, as −2<−161. (B) -1: Not in the range, as −1<−161. (C) 4: Is in the range, as 4≥3. (D) 7: Is in the range, as 7≥3.
Both options (C) and (D) satisfy the condition for k.
