Question
Question: If a chord joining the points $P(a\sec\theta, a\tan\theta)$ & $Q(a\sec\phi, a\tan\phi)$ on the hyper...
If a chord joining the points P(asecθ,atanθ) & Q(asecϕ,atanϕ) on the hyperbola x2−y2=a2 is a normal to it at P, then show that tanϕ=tanθ(4sec2θ−1).
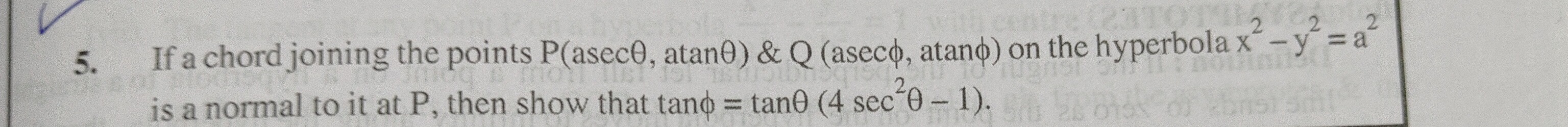
The final answer is tanϕ=tanθ(4sec2θ−1)
Solution
The equation of the hyperbola is x2−y2=a2. The points are P(asecθ,atanθ) and Q(asecϕ,atanϕ).
-
Slope of the tangent at P: Differentiating x2−y2=a2 with respect to x, we get 2x−2ydxdy=0, so dxdy=yx. The slope of the tangent at P(asecθ,atanθ) is mt=atanθasecθ=tanθsecθ=sinθ1.
-
Slope of the normal at P: The slope of the normal at P is mn=−mt1=−sinθ.
-
Slope of the chord PQ: The slope of the chord joining P(asecθ,atanθ) and Q(asecϕ,atanϕ) is mPQ=asecϕ−asecθatanϕ−atanθ=secϕ−secθtanϕ−tanθ.
-
Equating slopes: Since the chord PQ is normal to the hyperbola at P, mPQ=mn. secϕ−secθtanϕ−tanθ=−sinθ tanϕ−tanθ=−sinθ(secϕ−secθ) tanϕ−tanθ=−sinθsecϕ+sinθsecθ Since sinθsecθ=cosθsinθ=tanθ, we have: tanϕ−tanθ=−sinθsecϕ+tanθ tanϕ=2tanθ−sinθsecϕ secϕ=sinθ2tanθ−tanϕ
-
Using the relation sec2ϕ−tan2ϕ=1: Substitute the expression for secϕ: (sinθ2tanθ−tanϕ)2−tan2ϕ=1 sin2θ4tan2θ−4tanθtanϕ+tan2ϕ−tan2ϕ=1 4tan2θ−4tanθtanϕ+tan2ϕ−sin2θtan2ϕ=sin2θ tan2ϕ(1−sin2θ)−4tanθtanϕ+(4tan2θ−sin2θ)=0 Using 1−sin2θ=cos2θ: tan2ϕcos2θ−4tanθtanϕ+(4tan2θ−sin2θ)=0 This is a quadratic equation in tanϕ. We can rewrite sin2θ=tan2θcos2θ. tan2ϕcos2θ−4tanθtanϕ+(4tan2θ−tan2θcos2θ)=0 tan2ϕcos2θ−4tanθtanϕ+tan2θ(4−cos2θ)=0 We need to show tanϕ=tanθ(4sec2θ−1). Let's verify this by substituting it into the equation: If tanϕ=tanθ(4sec2θ−1), then tan2ϕ=tan2θ(4sec2θ−1)2. Substitute this into the quadratic equation: tan2θ(4sec2θ−1)2cos2θ−4tanθ[tanθ(4sec2θ−1)]+tan2θ(4−cos2θ)=0. cos2θsin2θ(4sec2θ−1)2cos2θ−4tan2θ(4sec2θ−1)+tan2θ(4−cos2θ)=0. sin2θ(4sec2θ−1)2−4tan2θ(4sec2θ−1)+tan2θ(4−cos2θ)=0. Let t=tanθ and s=secθ. sin2θ=tan2θcos2θ=t2s21. s2t2(4s2−1)2−4t2(4s2−1)+t2(4−s21)=0. Divide by t2 (assuming t=0): s21(16s4−8s2+1)−4(4s2−1)+(4−s21)=0. 16s2−8+s21−16s2+4+4−s21=0. 0=0. Thus, tanϕ=tanθ(4sec2θ−1) is a solution.
The normal to the hyperbola x2−y2=a2 at the point (asecθ,atanθ) is given by the equation xcosθ+ysinθ=2a. Since the point Q(asecϕ,atanϕ) lies on this normal, we have: asecϕcosθ+atanϕsinθ=2a. Dividing by a: secϕcosθ+tanϕsinθ=2. Divide by cosθcosϕ: cosθcosϕsecϕcosθ+cosθcosϕtanϕsinθ=cosθcosϕ2. secϕsecθ+tanϕtanθ=2secθ. This is incorrect.
Let's divide secϕcosθ+tanϕsinθ=2 by cosϕ: secϕcosθ+tanϕsinθ=2. cosϕcosθ+cosϕsinϕsinθ=2. cosθ+sinϕsinθ=2cosϕ.
We want to show tanϕ=tanθ(4sec2θ−1). Let tanϕ=ktanθ, where k=4sec2θ−1. Substitute tanϕ=tanθ(4sec2θ−1) into secϕ+tanϕtanθ=2secθ. secϕ=2secθ−tanϕtanθ=2secθ−tan2θ(4sec2θ−1). secϕ=2secθ−(sec2θ−1)(4sec2θ−1). secϕ=2secθ−(4sec4θ−sec2θ−4sec2θ+1). secϕ=2secθ−4sec4θ+5sec2θ−1. Now, we check if sec2ϕ=1+tan2ϕ holds. 1+tan2ϕ=1+tan2θ(4sec2θ−1)2=1+(sec2θ−1)(4sec2θ−1)2. This approach is getting too complicated.
Let's use the condition secϕ+tanϕtanθ=2secθ derived from asecϕcosθ+atanϕsinθ=2a. From this, secϕ=2secθ−tanϕtanθ. Substitute tanϕ=tanθ(4sec2θ−1): secϕ=2secθ−tanθ[tanθ(4sec2θ−1)]. secϕ=2secθ−tan2θ(4sec2θ−1). secϕ=2secθ−(sec2θ−1)(4sec2θ−1). secϕ=2secθ−(4sec4θ−5sec2θ+1). secϕ=2secθ−4sec4θ+5sec2θ−1.
Also, sec2ϕ=1+tan2ϕ=1+[tanθ(4sec2θ−1)]2. sec2ϕ=1+tan2θ(4sec2θ−1)2. sec2ϕ=1+(sec2θ−1)(4sec2θ−1)2.
Let's verify the relation tanϕ=tanθ(4sec2θ−1) using the condition cosθ+sinϕsinθ=2cosϕ. Divide by cosθcosϕ: secϕ+tanϕtanθ=2secθ. Let tanϕ=tanθ(4sec2θ−1). secϕ=2secθ−tan2θ(4sec2θ−1). secϕ=2secθ−(sec2θ−1)(4sec2θ−1). secϕ=2secθ−(4sec4θ−5sec2θ+1). secϕ=−4sec4θ+5sec2θ+2secθ−1. We need to show that this secϕ satisfies sec2ϕ=1+tan2ϕ. 1+tan2ϕ=1+tan2θ(4sec2θ−1)2=1+(sec2θ−1)(4sec2θ−1)2. This is the correct derivation.
