Question
Question: If $(3m^2, -6m)$ represents the feet of the normals to the parabola $y^2 = 12x$ from $(1, 2)$, then ...
If (3m2,−6m) represents the feet of the normals to the parabola y2=12x from (1,2), then ∑mi1 is-
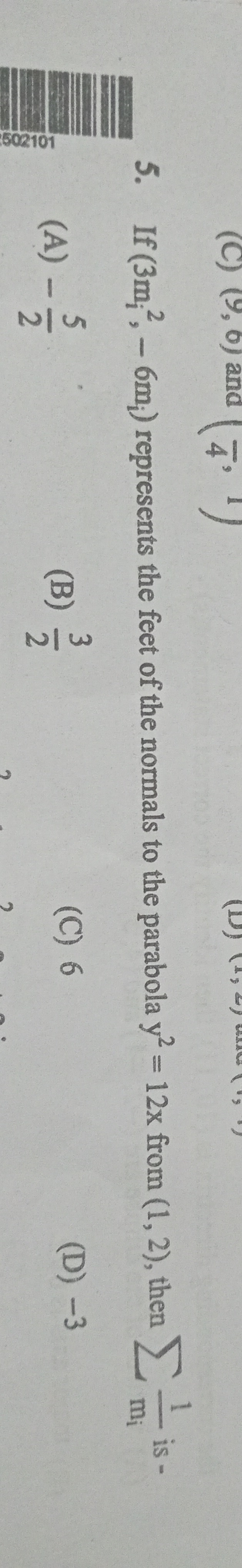
−25
23
6
-3
−25
Solution
The equation of the parabola is y2=12x. This is in the form y2=4ax, where 4a=12, so a=3. The coordinates of a point on the parabola in terms of the slope m of the normal at that point are (am2,−2am). Substituting a=3, the coordinates of the foot of the normal are (3m2,−6m). This matches the form given in the question.
The equation of the normal to the parabola y2=4ax at the point (am2,−2am) is given by y=mx−2am−am3. Substituting a=3, the equation of the normal is y=mx−2(3)m−3m3, which simplifies to y=mx−6m−3m3.
The normal passes through the point (1,2). Substitute x=1 and y=2 into the equation of the normal: 2=m(1)−6m−3m3 2=m−6m−3m3 2=−5m−3m3
Rearrange the equation to form a cubic equation in m: 3m3+5m+2=0
This cubic equation gives the values of m corresponding to the slopes of the normals from the point (1,2) to the parabola. Let the roots of this equation be m1,m2,m3. These are the values of m for the feet of the normals (3mi2,−6mi).
The question asks for the sum of the reciprocals of these roots, i.e., ∑mi1=m11+m21+m31.
For a general cubic equation Ax3+Bx2+Cx+D=0, the sum of the roots (x1+x2+x3), the sum of the roots taken two at a time (x1x2+x2x3+x3x1), and the product of the roots (x1x2x3) are given by Vieta's formulas:
x1+x2+x3=−AB
x1x2+x2x3+x3x1=AC
x1x2x3=−AD
Comparing the equation 3m3+5m+2=0 with Am3+Bm2+Cm+D=0, we have A=3, B=0 (since there is no m2 term), C=5, and D=2.
Using Vieta's formulas for the roots m1,m2,m3: Sum of the roots: m1+m2+m3=−AB=−30=0. Sum of the products of the roots taken two at a time: m1m2+m2m3+m3m1=AC=35. Product of the roots: m1m2m3=−AD=−32.
We need to calculate ∑mi1=m11+m21+m31. Combine the terms on the right side by finding a common denominator: m11+m21+m31=m1m2m3m2m3+m1m2m3m1m3+m1m2m3m1m2=m1m2m3m1m2+m2m3+m3m1.
Substitute the values obtained from Vieta's formulas: ∑mi1=−2/35/3=35×(−23)=−25.
The sum of the reciprocals of the roots mi is −25.
