Question
Question: If $0 < \theta, \phi < \frac{\pi}{2}, x = \sum_{n=0}^{\infty} \cos^{2n}\theta, y = \sum_{n=0}^{\inft...
If 0<θ,ϕ<2π,x=∑n=0∞cos2nθ,y=∑n=0∞sin2nϕ and z=∑n=0∞cos2nθsin2nϕ then:
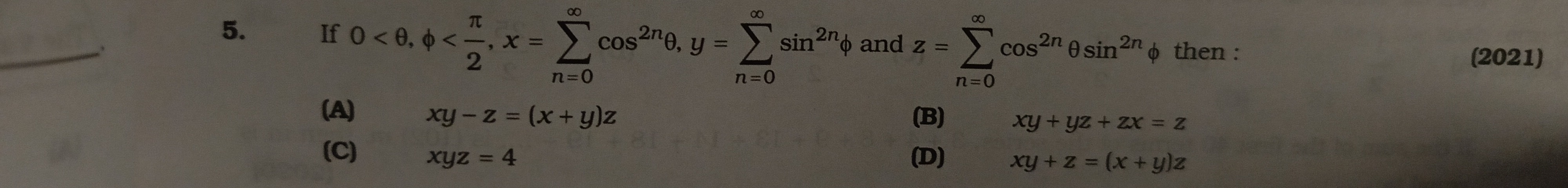
xy - z = (x + y)z
xy + yz + zx = z
xyz = 4
xy + z = (x + y)z
xy + z = (x + y)z
Solution
The problem requires evaluating three infinite geometric series and then finding the correct relationship between the resulting variables x, y, and z.
1. Evaluating the Series: The sum of an infinite geometric series is given by the formula S=1−ra, where a is the first term and r is the common ratio, provided that ∣r∣<1.
-
For x=∑n=0∞cos2nθ: The first term (a) is cos2×0θ=cos0θ=1. The common ratio (r) is cos2θ. Given 0<θ<2π, we know that 0<cosθ<1, which implies 0<cos2θ<1. Thus, ∣r∣<1, and the series converges. Therefore, x=1−cos2θ1. Using the fundamental trigonometric identity sin2θ+cos2θ=1, we have 1−cos2θ=sin2θ. So, x=sin2θ1.
-
For y=∑n=0∞sin2nϕ: The first term (a) is sin2×0ϕ=sin0ϕ=1. The common ratio (r) is sin2ϕ. Given 0<ϕ<2π, we know that 0<sinϕ<1, which implies 0<sin2ϕ<1. Thus, ∣r∣<1, and the series converges. Therefore, y=1−sin2ϕ1. Using the identity sin2ϕ+cos2ϕ=1, we have 1−sin2ϕ=cos2ϕ. So, y=cos2ϕ1.
-
For z=∑n=0∞cos2nθsin2nϕ: This series can be rewritten as z=∑n=0∞(cos2θsin2ϕ)n. The first term (a) is (cos2θsin2ϕ)0=1. The common ratio (r) is cos2θsin2ϕ. Since 0<cos2θ<1 and 0<sin2ϕ<1, their product 0<cos2θsin2ϕ<1. Thus, ∣r∣<1, and the series converges. Therefore, z=1−cos2θsin2ϕ1.
2. Expressing Trigonometric Terms in terms of x and y: From the expressions for x and y:
-
x=sin2θ1⟹sin2θ=x1. Using cos2θ=1−sin2θ, we get cos2θ=1−x1=xx−1.
-
y=cos2ϕ1⟹cos2ϕ=y1. Using sin2ϕ=1−cos2ϕ, we get sin2ϕ=1−y1=yy−1.
3. Substituting into the expression for z: Now, substitute the expressions for cos2θ and sin2ϕ into the formula for z: z=1−cos2θsin2ϕ1=1−(xx−1)(yy−1)1 To simplify the denominator: 1−xy(x−1)(y−1)=xyxy−(x−1)(y−1) =xyxy−(xy−x−y+1) =xyxy−xy+x+y−1 =xyx+y−1
So, z=xyx+y−11=x+y−1xy.
4. Rearranging the Relationship: The derived relationship is z=x+y−1xy. Multiply both sides by (x+y−1): z(x+y−1)=xy zx+zy−z=xy
5. Checking the Options: We need to find which of the given options is equivalent to xy=z(x+y−1).
-
(A) xy−z=(x+y)z xy−z=xz+yz xy=xz+yz+z xy=z(x+y+1) This does not match our derived equation.
-
(B) xy+yz+zx=z xy=z−yz−zx xy=z(1−y−x) This does not match our derived equation.
-
(C) xyz=4 This option suggests a constant numerical relationship. However, the values of x, y, and z depend on θ and ϕ. For example, if θ=π/4 and ϕ=π/4: cos2(π/4)=(1/2)2=1/2. sin2(π/4)=(1/2)2=1/2. x=∑n=0∞(1/2)n=1−1/21=2. y=∑n=0∞(1/2)n=1−1/21=2. z=∑n=0∞(1/2×1/2)n=∑n=0∞(1/4)n=1−1/41=3/41=4/3. In this case, xyz=2×2×4/3=16/3=4. So, this option is incorrect.
-
(D) xy+z=(x+y)z xy+z=xz+yz xy=xz+yz−z xy=z(x+y−1) This exactly matches our derived relationship.
Therefore, the correct option is (D).
