Question

5 girls and 10 boys sit at random in a row having 15 chairs numbered as 1 to 15, then the probability that end seats are occupied by the girls and between any two girls and odd number of boy sit is
A. $\dfrac{{20 \times 10! \times 5!}}{{15!}}$
B. $\dfrac{{10 \times 10! \times 5!}}{{15!}}$
C. $\dfrac{{20 \times 10! \times 30!}}{{15!}}$
D. $\dfrac{{10 \times 10! \times 5!}}{{25!}}$

Answer 1

We will first find the total number of ways in which all the given girls and boys arrange themselves. Then, according to the given condition, there are 4 gaps in which an odd number of boys can sit. Form an equation and find the possible number of solutions for it. Next, multiply the ways in which boys and girls can arrange among themselves. At last apply the formula , $\dfrac{{{\text{Number of favourable outcomes}}}}{{{\text{total number of outcomes}}}}$ to find the required probability.

Complete step-by-step answer:
When there are $n$ objects and $n$ places, then the number of ways in which objects can be arranged is $n!$.
There are a total of 15 people and 15 seats, then the total number of ways in which the person can be seated is 15!
We have to find the probability that end seats are occupied by the girls and between any two girls and an odd number of boys sit.
Since, girls sit at the ends.

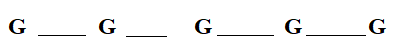
There are four gaps between girls where boys can sit.
But, we want an odd number of boys to sit there.
Let the number of boys in the gaps be $2a + 1$, $2b + 1$, $2c + 1$ and $2d + 1$
Now, there are 10 total boys,
$2a + 1 + 2b + 1 + 2c + 1 + 2d + 1 = 10 \\\ \Rightarrow 2a + 2b + 2c + 2d = 6 \\\ \Rightarrow a + b + c + d = 3 \\\$
Now, the values of $a,b,c,d$ have to be integers.
Number of solutions possible for an equation, coefficient of ${x^3}$ in $\left( {1 - {x^4}} \right)$ is $^6{C_3}$
We know that $^n{C_r} = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}$
That is, $^6{C_3} = \dfrac{{6!}}{{3!\left( 3 \right)!}} = \dfrac{{6.5.4.3!}}{{3!\left( 3 \right)!}} = 20$
But, all 5 three girls and 10 boys can also arrange among themselves
Hence, the total number of ways in which that end seats are occupied by the girls and between any two girls and odd number of boys sit is $20 \times 5! \times 10!$
We know that probability of an event is equal to $\dfrac{{{\text{Number of favourable outcomes}}}}{{{\text{total number of outcomes}}}}$
Then, the required probability is $\dfrac{{20 \times 10! \times 5!}}{{15!}}$
Hence, option A is correct.

Note: The probability of an event is never less than 0 or greater than 1. When the order of arrangement does not matter, we use combination but when the order of the arrangement matters, we use permutation. Here, after finding total combinations, we have multiplied with the permutation when boys and girls arrange among themselves.