Question

Find the points of the parabola $y^2=4ax$ at which the normal is inclined at $30^\circ$ to the ax

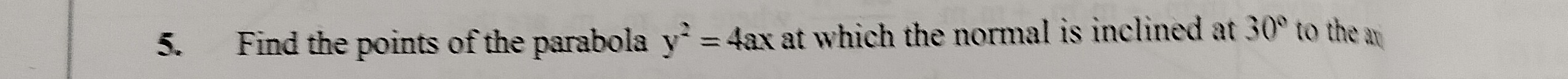
• A. The points are $\left(\frac{a}{3}, \frac{2a}{\sqrt{3}}\right)$ and $\left(\frac{a}{3}, -\frac{2a}{\sqrt{3}}\right)$
• B. The points are $\left(\frac{a}{3}, \frac{2a}{\sqrt{3}}\right)$
• C. The points are $\left(\frac{a}{3}, -\frac{2a}{\sqrt{3}}\right)$
• D. The points are $\left(\frac{a}{3}, 0\right)$

Answer 1

Answer: (A)

The points are $\left(\frac{a}{3}, \frac{2a}{\sqrt{3}}\right)$ and $\left(\frac{a}{3}, -\frac{2a}{\sqrt{3}}\right)$

Answer 2

The points on the parabola $y^2=4ax$ can be represented parametrically as $(at^2, 2at)$. The slope of the tangent at a point $(at^2, 2at)$ is $m_t = \frac{1}{t}$. The slope of the normal is $m_n = -t$. If the normal is inclined at $30^\circ$ to the x-axis, its slope can be $\tan(30^\circ) = \frac{1}{\sqrt{3}}$ or $\tan(180^\circ - 30^\circ) = -\frac{1}{\sqrt{3}}$.

Case 1: $m_n = \frac{1}{\sqrt{3}}$ $-t = \frac{1}{\sqrt{3}} \implies t = -\frac{1}{\sqrt{3}}$. The point is $(a(-\frac{1}{\sqrt{3}})^2, 2a(-\frac{1}{\sqrt{3}})) = (\frac{a}{3}, -\frac{2a}{\sqrt{3}})$.

Case 2: $m_n = -\frac{1}{\sqrt{3}}$ $-t = -\frac{1}{\sqrt{3}} \implies t = \frac{1}{\sqrt{3}}$. The point is $(a(\frac{1}{\sqrt{3}})^2, 2a(\frac{1}{\sqrt{3}})) = (\frac{a}{3}, \frac{2a}{\sqrt{3}})$.

Thus, the points are $\left(\frac{a}{3}, \frac{2a}{\sqrt{3}}\right)$ and $\left(\frac{a}{3}, -\frac{2a}{\sqrt{3}}\right)$.