Question

Find the equation of directrix, co-ordinate of foci, centre, vertices, length of latus and eccentricity of ellipse $\sqrt{(x-6)^2+(y-2)^2} + \sqrt{(x)^2+(y-2)^2} = 10.$

Answer 1

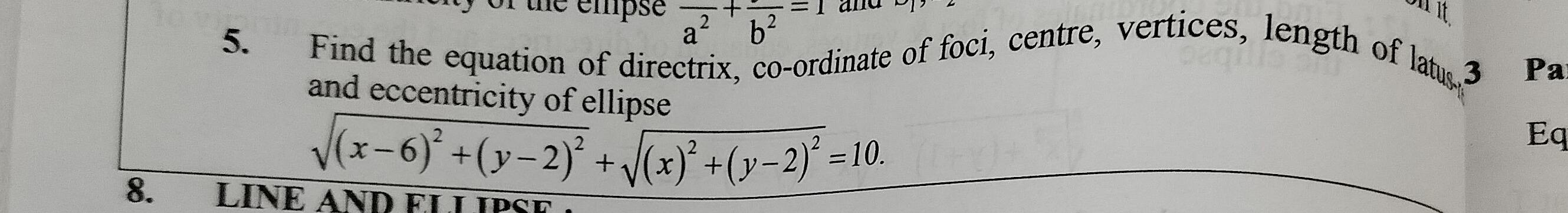
• Centre: $(3, 2)$
• Co-ordinate of Foci: $(6, 2)$ and $(0, 2)$
• Vertices: $(8, 2)$ and $(-2, 2)$
• Length of Latus Rectum: $\frac{32}{5}$
• Eccentricity: $\frac{3}{5}$
• Equations of Directrices: $x = \frac{34}{3}$ and $x = -\frac{16}{3}$

Answer 2

The given equation $\sqrt{(x-6)^2+(y-2)^2} + \sqrt{x^2+(y-2)^2} = 10$ represents the locus of a point $P(x, y)$ such that the sum of its distances from two fixed points (foci) is constant. The two fixed points are $F_1 = (6, 2)$ and $F_2 = (0, 2)$. The constant sum of distances is $10$.

This is the definition of an ellipse, where: The foci are $F_1(6, 2)$ and $F_2(0, 2)$. The constant sum of distances is $2a = 10$, which implies the semi-major axis length $a = 5$.

The distance between the foci is $2c$. $2c = \sqrt{(6-0)^2 + (2-2)^2} = \sqrt{6^2 + 0^2} = 6$. So, $c = 3$.

The center of the ellipse is the midpoint of the line segment joining the foci. Center $(h, k) = \left(\frac{6+0}{2}, \frac{2+2}{2}\right) = \left(\frac{6}{2}, \frac{4}{2}\right) = (3, 2)$.

For an ellipse, the relationship between $a$, $b$ (semi-minor axis), and $c$ is $a^2 = b^2 + c^2$. Substituting the values of $a$ and $c$: $5^2 = b^2 + 3^2$ $25 = b^2 + 9$ $b^2 = 25 - 9 = 16$ $b = 4$.

Since the y-coordinates of the foci are the same ($y=2$), the major axis is horizontal. The standard equation of an ellipse with a horizontal major axis and center $(h, k)$ is: $\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$ Substituting the values $h=3$, $k=2$, $a=5$, and $b=4$: $\frac{(x-3)^2}{5^2} + \frac{(y-2)^2}{4^2} = 1$ $\frac{(x-3)^2}{25} + \frac{(y-2)^2}{16} = 1$

Now, we find the required properties:

1. Centre: The center is $(h, k) = (3, 2)$.

2. Co-ordinate of Foci: For a horizontal major axis, the foci are at $(h \pm c, k)$. Foci are $(3 \pm 3, 2)$. $F_1 = (3+3, 2) = (6, 2)$ $F_2 = (3-3, 2) = (0, 2)$

3. Vertices: For a horizontal major axis, the vertices are at $(h \pm a, k)$. Vertices are $(3 \pm 5, 2)$. $V_1 = (3+5, 2) = (8, 2)$ $V_2 = (3-5, 2) = (-2, 2)$

4. Length of Latus Rectum: The length of the latus rectum is given by $\frac{2b^2}{a}$. Length $= \frac{2 \times 16}{5} = \frac{32}{5}$.

5. Eccentricity: Eccentricity $e$ is given by $e = \frac{c}{a}$. $e = \frac{3}{5}$.

6. Equation of Directrix: For a horizontal major axis, the equations of the directrices are $x = h \pm \frac{a}{e}$. $x = 3 \pm \frac{5}{3/5}$ $x = 3 \pm \frac{25}{3}$ The two equations of the directrices are: $x_1 = 3 + \frac{25}{3} = \frac{9+25}{3} = \frac{34}{3}$ $x_2 = 3 - \frac{25}{3} = \frac{9-25}{3} = -\frac{16}{3}$