Solveeit Logo
Login

Question

Question: Evaluate: $\lim_{m\to\infty} \left(m^3 \int_m^{2m} \frac{xdx}{x^5+1}\right)$, $(m \in N, 0<x<1)$...

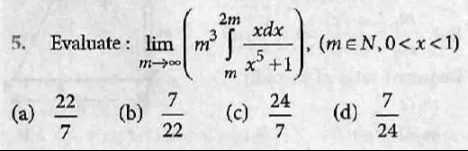
Evaluate: lim⁡m→∞(m3∫m2mxdxx5+1)\lim_{m\to\infty} \left(m^3 \int_m^{2m} \frac{xdx}{x^5+1}\right), (m∈N,0<x<1)(m \in N, 0<x<1)

A

227\frac{22}{7}

B

722\frac{7}{22}

C

247\frac{24}{7}

D

724\frac{7}{24}

Answer

724\frac{7}{24}

Explanation

Solution

For large xx, note that:

x5+1≈x5⟹xx5+1≈xx5=1x4.x^5 + 1 \approx x^5 \quad \Longrightarrow \quad \frac{x}{x^5+1} \approx \frac{x}{x^5}=\frac{1}{x^4}.

Thus:

∫m2mxx5+1 dx≈∫m2mdxx4.\int_m^{2m}\frac{x}{x^5+1}\,dx \approx \int_m^{2m}\frac{dx}{x^4}.

Evaluating the approximate integral:

∫dxx4=−13x3+C.\int \frac{dx}{x^4} = -\frac{1}{3x^3} + C.

So,

∫m2mdxx4=[−13x3]m2m=−13(2m)3+13m3=13m3−124m3=8−124m3=724m3.\int_m^{2m}\frac{dx}{x^4} = \left[-\frac{1}{3x^3}\right]_m^{2m} = -\frac{1}{3(2m)^3} + \frac{1}{3m^3} = \frac{1}{3m^3} - \frac{1}{24m^3} = \frac{8-1}{24m^3} = \frac{7}{24m^3}.

Multiplying by m3m^3:

m3∫m2mxx5+1 dx≈m3⋅724m3=724.m^3 \int_m^{2m}\frac{x}{x^5+1}\,dx \approx m^3 \cdot \frac{7}{24m^3} = \frac{7}{24}.

Taking the limit as m→∞m\to\infty gives:

lim⁡m→∞(m3∫m2mxx5+1 dx)=724.\lim_{m\to\infty}\left(m^3\int_m^{2m}\frac{x}{x^5+1}\,dx\right) = \frac{7}{24}.