Question

Calculate the angle $\theta$ for which if the particle A is released, it undergoes perfectly elastic collision with another identical mass B placed at rest and B is found to just reach the horizontal position of its string.

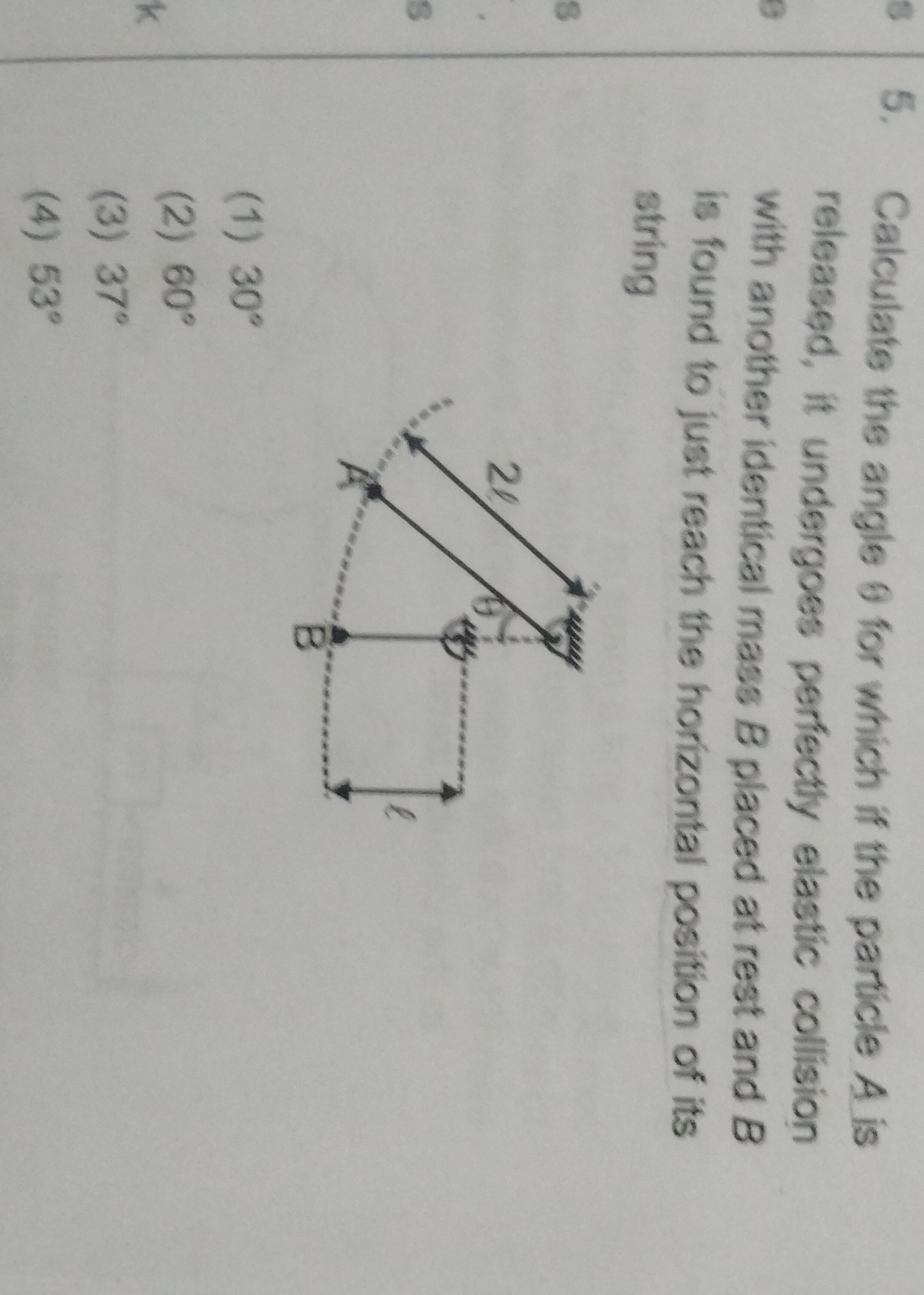
• A. 30°
• B. 60°
• C. 37°
• D. 53°

Answer 1

Answer: (B)

60°

Answer 2

The problem involves two main physical principles: conservation of mechanical energy and elastic collision.

1. Velocity of particle A just before collision:

   Particle A is released from rest at an angle $\theta$. Its string length is $L_A = 2l$. The vertical height dropped by particle A is $h_A = L_A - L_A \cos \theta = 2l(1 - \cos \theta)$. Using the principle of conservation of mechanical energy, the potential energy at the initial position is converted into kinetic energy at the lowest point (just before collision).

   $m_A g h_A = \frac{1}{2} m_A v_A^2$

   $m_A g [2l(1 - \cos \theta)] = \frac{1}{2} m_A v_A^2$

   $v_A^2 = 4gl(1 - \cos \theta)$

   $v_A = \sqrt{4gl(1 - \cos \theta)}$

2. Velocities after the perfectly elastic collision:

   The collision is perfectly elastic and involves two identical masses ($m_A = m_B = m$). Particle B is initially at rest. In a perfectly elastic collision between two identical masses, if one is initially at rest, they exchange velocities. Therefore, after the collision:

   • Velocity of particle A ($v_A'$) = 0 (particle A comes to rest)
   • Velocity of particle B ($v_B'$) = $v_A$ (particle B moves with the initial velocity of A)

   So, $v_B' = \sqrt{4gl(1 - \cos \theta)}$.

3. Velocity required for particle B to just reach the horizontal position:

   Particle B has a string length of $L_B = l$. To just reach the horizontal position, its final height must be $h_B = l$ (relative to its lowest point). Using the principle of conservation of mechanical energy for particle B after the collision: The kinetic energy of particle B at the lowest point is converted into potential energy at the horizontal position.

   $\frac{1}{2} m_B (v_B')^2 = m_B g h_B$

   $\frac{1}{2} m (v_B')^2 = m g l$

   $(v_B')^2 = 2gl$

   $v_B' = \sqrt{2gl}$

4. Solving for the angle $\theta$:

   Equating the expressions for $v_B'$ from step 2 and step 3:

   $\sqrt{4gl(1 - \cos \theta)} = \sqrt{2gl}$

   Squaring both sides:

   $4gl(1 - \cos \theta) = 2gl$

   Divide both sides by $2gl$:

   $2(1 - \cos \theta) = 1$

   $1 - \cos \theta = \frac{1}{2}$

   $\cos \theta = 1 - \frac{1}{2}$

   $\cos \theta = \frac{1}{2}$

   Therefore, $\theta = 60^\circ$.