Question

5 boys and 3 girls sit in a row at random. The probability that no girls sit together is
A. $\dfrac{3}{{14}}$
B. $\dfrac{5}{{14}}$
C. $\dfrac{9}{{14}}$
D. $\dfrac{7}{{14}}$

Answer 1

We will first find the total number of ways in which all people can be arranged. Then, find the number of ways in which 3 girls can sit together by considering all three girls as a single unit. And at last, subtract the number of ways in which three girls together from the total number of ways in all persons can be arranged.

Complete step-by-step answer:
When there are $n$ objects and $n$ places, then the number of ways in which objects can be arranged is $n!$.
There are total 8 person and 8 seats, then the total number of ways in which the person can be seated is $8!$
Also, we know $n! = n.\left( {n - 1} \right).\left( {n - 2} \right).....3.2.1$.
Then, total possible outcomes are $8! = 8.7.6.5.4.3.2.1 = 40320$,
But, we need that no two girls sit side by side.
Then, there has to be a girl between every two boys.

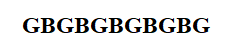
Here, we can see there are 6 positions that a girl can occupy.
Then, 3 girls can choose any of the six positions.
We will use combinations to find the number of ways in which 3 girls can be seated when no two girls can sit together.
Hence, there are $^6{C_3}$
Also, $^n{C_r} = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}$
Then, $^6{C_3} = \dfrac{{6!}}{{3!\left( 3 \right)!}} = \dfrac{{6.5.4.3!}}{{3.2.1.3!}} = 20$
Also, the three girls and 5 boys can arrange among themselves.
Therefore, total ways in which two girls can sit such that no girls sit together.
$5!3!\left( {20} \right) = 5.4.3.2.1.3.2.1.20 = 14400$
We will calculate the probability by dividing the number of favourable outcomes by the total number of all the possible outcomes.
$\dfrac{{14400}}{{40320}} = \dfrac{5}{{14}}$
Hence, option B is correct.

Note: When there are $n$ distinct objects and needs to be arranged in $n$ places, then the number of ways in which these can be arranged is $n!$. Also, $n! = n.\left( {n - 1} \right).\left( {n - 2} \right).....3.2.1$. Since, the position of the girls and boys will also matter that’s why we have to multiply 3! and 5! by finding the total ways of arrangement.