Question

Board-(a) is lying on top of board-(b). Together, they form a single unit and move with some velocity v on a smooth horizontal surface. They collide with another identical board-(c). There is no friction between boards-(a) and (b), but there is friction between boards-(a) and (c). Upon collision, boards-(b) and (c) are firmly coupled and do not move relative to each other. The length of each board is L. Board -(a) stops moving relative to board-(b) and (c) at the moment it is entirely located on top of board-(c). Find the displacement ∆x of board (a) from the moment of collision until the relative motion of the boards stops. If the value of ∆x is $\frac{\alpha L}{21}$, the value of $\alpha$ is. Take : $\pi = \frac{22}{7}$.

Answer 1

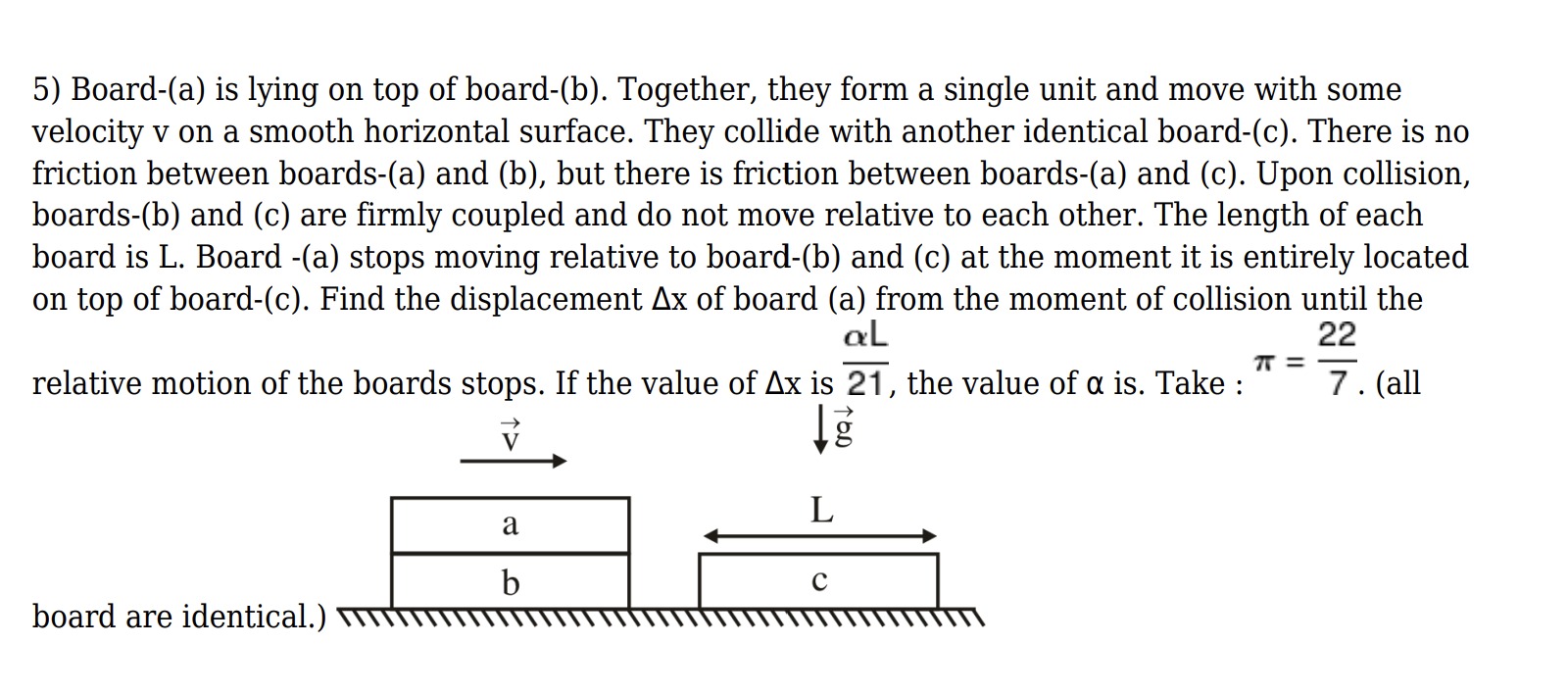
70

Answer 2

Let $m$ be the mass of each board. Initially, board (a) and (b) together have a mass of $2m$ and velocity $v$. Board (c) has mass $m$ and velocity 0. The collision is between the unit (a+b) and (c). Upon collision, boards (b) and (c) are firmly coupled. Let the velocity of board (a) immediately after the collision be $v_a'$ and the velocity of the coupled boards (b) and (c) be $v_{bc}'$.

By conservation of momentum for the system (a+b+c) during the collision: $(m+m)v + m(0) = mv_a' + (m+m)v_{bc}'$ $2mv = mv_a' + 2mv_{bc}'$ $2v = v_a' + 2v_{bc}' \quad (1)$

After the collision, board (a) is on top of board (b), and boards (b) and (c) are coupled. There is friction between boards (a) and (c). Since (b) and (c) are coupled, the friction is between board (a) and the combined board (b+c). Let the coefficient of kinetic friction between (a) and (c) be $\mu$. The normal force between (a) and (c) is $mg$. The friction force is $f_k = \mu mg$. This force acts on (a) and (b+c) in opposite directions.

The motion continues until board (a) stops moving relative to board (b) and (c), which means their velocities become equal. Let the final common velocity be $v_{final}$.

By conservation of momentum for the system (a+b+c) from immediately after collision until relative motion stops: $mv_a' + 2mv_{bc}' = m v_{final} + 2m v_{final} = 3m v_{final}$ From equation (1), $2mv = 3m v_{final}$, so $v_{final} = \frac{2v}{3}$.

Now, let's analyze the motion using the work-energy theorem or by considering the work done by friction. The work done by friction on the system is dissipated as heat and also changes the kinetic energy.

Consider the motion of board (a) relative to the coupled board (b+c). Let the relative displacement of (a) with respect to (b+c) be $\Delta x_{rel}$. The friction force on (a) is $f_a = -\mu mg$ (assuming $v_a > v_{bc}$). The friction force on (b+c) is $f_{bc} = +\mu mg$.

The work done by friction is $W_{friction} = \int \vec{f}_a \cdot d\vec{r}_a + \int \vec{f}_{bc} \cdot d\vec{r}_{bc} = \int \vec{f}_a \cdot (d\vec{r}_a - d\vec{r}_{bc}) = \int \vec{f}_a \cdot d\vec{r}_{rel}$.

Since the friction force on (a) is opposite to the relative velocity, the work done by friction on the relative motion is $W_{rel} = -\mu mg |\Delta x_{rel}|$. This work is dissipated as heat.

The total work done by friction on the system is $W_{friction} = W_a + W_{bc}$. The work done by friction on the system is equal to the change in kinetic energy of the system.

$W_{friction} = K_{final} - K_{initial} = (\frac{1}{2} m v_{final}^2 + \frac{1}{2} (2m) v_{final}^2) - (\frac{1}{2} m v_a'^2 + \frac{1}{2} (2m) v_{bc}'^2)$ $W_{friction} = \frac{3}{2} m (\frac{2v}{3})^2 - (\frac{1}{2} m v_a'^2 + m v_{bc}'^2) = \frac{2}{3} m v^2 - \frac{1}{2} m v_a'^2 - m v_{bc}'^2$.

The work done by friction is also equal to the energy dissipated due to relative motion. The work done by friction on the system is $W_{friction} = -\text{Energy dissipated} = -\mu mg |\Delta x_{rel}|$. So, $-\mu mg |\Delta x_{rel}| = \frac{2}{3} m v^2 - \frac{1}{2} m v_a'^2 - m v_{bc}'^2$. $|\Delta x_{rel}| = \frac{1}{\mu g} (\frac{1}{2} v_a'^2 + v_{bc}'^2 - \frac{2}{3} v^2)$.

We need to find $v_a'$ and $v_{bc}'$. Let's assume the collision between (a+b) and (c) is such that momentum is conserved and the impulse on (a) is negligible compared to the impulse between (b) and (c). So, immediately after the collision, $v_a' \approx v$. However, this contradicts the fact that (a) slides relative to (b) and (c) and eventually stops relative to them.

Let's consider the collision as an interaction between the combined block (a+b) and (c), where (b) and (c) stick together. This is an inelastic collision between (a+b) and (c) where (b) and (c) form a single body after collision.

Let's assume that during the collision, the impulse between (a) and (b) is negligible (no friction) and the impulse between (a) and (c) is also negligible during the very short collision time. The main impulse is between (b) and (c). Consider the momentum of (a) and (b+c) immediately after the collision.

Let's assume that the relative velocity of separation between (a) and (b+c) is related to the initial relative velocity of approach between (a+b) and (c). However, the collision is between (a+b) and (c).

Let's consider the collision as an inelastic collision between (b) and (c), where (a) is just on top of (b) and the friction between (a) and (c) acts after the collision. If the collision is only between (b) and (c), and they stick together, then by conservation of momentum of (b+c) assuming (a) is not involved in the collision impulse: $mv + m(0) = (m+m)v_{bc}'$, so $mv = 2mv_{bc}'$, $v_{bc}' = v/2$. If (a) continues with velocity $v$, then $v_a' = v$. In this case, $v_a' = v$ and $v_{bc}' = v/2$. Check momentum conservation for the whole system: $mv_a' + 2mv_{bc}' = mv + 2m(v/2) = mv + mv = 2mv$. This is consistent with the initial momentum. So, let's assume immediately after the collision, $v_a' = v$ and $v_{bc}' = v/2$. The final velocity is $v_{final} = 2v/3$. The relative velocity immediately after collision is $v_{rel,0} = v_a' - v_{bc}' = v - v/2 = v/2$. The relative velocity at time $t$ is $v_{rel}(t) = v_{rel,0} + \int_0^t \frac{dv_{rel}}{dt'} dt' = v/2 - \frac{3\mu g}{2} t$. Relative motion stops when $v_{rel}(t) = 0$, so $t_{stop} = \frac{v/2}{3\mu g/2} = \frac{v}{3\mu g}$.

Now we need to find the displacement $\Delta x$ of board (a) from the moment of collision until relative motion stops. The velocity of board (a) at time $t$ is $v_a(t) = v_a' + \int_0^t \frac{dv_a}{dt'} dt' = v - \mu g t$. The displacement of board (a) is $\Delta x = \int_0^{t_{stop}} v_a(t) dt = \int_0^{v/(3\mu g)} (v - \mu g t) dt = [vt - \frac{1}{2} \mu g t^2]_0^{v/(3\mu g)}$ $\Delta x = v \frac{v}{3\mu g} - \frac{1}{2} \mu g (\frac{v}{3\mu g})^2 = \frac{v^2}{3\mu g} - \frac{1}{2} \mu g \frac{v^2}{9\mu^2 g^2} = \frac{v^2}{3\mu g} - \frac{v^2}{18\mu g} = \frac{6v^2 - v^2}{18\mu g} = \frac{5v^2}{18\mu g}$.

Let's find the relative displacement $\Delta x_{rel} = |\Delta x_a - \Delta x_{bc}|$. Velocity of (b+c) at time $t$ is $v_{bc}(t) = v_{bc}' + \int_0^t \frac{dv_{bc}}{dt'} dt' = v/2 + \frac{\mu g}{2} t$. Displacement of (b+c) is $\Delta x_{bc} = \int_0^{t_{stop}} v_{bc}(t) dt = \int_0^{v/(3\mu g)} (v/2 + \frac{\mu g}{2} t) dt = [\frac{v}{2} t + \frac{1}{4} \mu g t^2]_0^{v/(3\mu g)}$ $\Delta x_{bc} = \frac{v}{2} \frac{v}{3\mu g} + \frac{1}{4} \mu g (\frac{v}{3\mu g})^2 = \frac{v^2}{6\mu g} + \frac{1}{4} \mu g \frac{v^2}{9\mu^2 g^2} = \frac{v^2}{6\mu g} + \frac{v^2}{36\mu g} = \frac{6v^2 + v^2}{36\mu g} = \frac{7v^2}{36\mu g}$. The relative displacement is $\Delta x_{rel} = \Delta x - \Delta x_{bc} = \frac{5v^2}{18\mu g} - \frac{7v^2}{36\mu g} = \frac{10v^2 - 7v^2}{36\mu g} = \frac{3v^2}{36\mu g} = \frac{v^2}{12\mu g}$. Since $v_a' > v_{bc}'$, the relative velocity is positive, and the relative displacement is in the direction of relative velocity. So the relative displacement of (a) with respect to (b+c) is $\frac{v^2}{12\mu g}$.

The problem states that board (a) stops moving relative to board (b) and (c) at the moment it is entirely located on top of board-(c). This means that the relative displacement of (a) with respect to (b+c) is equal to the length of board (c), which is L, minus some initial overlap. However, the diagram shows that initially (a) is entirely on top of (b). When (a) is entirely on top of (c), it means (a) has moved a distance L relative to (b+c). So, $|\Delta x_{rel}| = L$. Thus, $L = \frac{v^2}{12\mu g}$. This gives a relation between $v$, $\mu$, $g$, and $L$.

We need to find the displacement $\Delta x$ of board (a) from the moment of collision until the relative motion of the boards stops. We found $\Delta x = \frac{5v^2}{18\mu g}$. Substitute $v^2 = 12\mu g L$ into the expression for $\Delta x$: $\Delta x = \frac{5}{18\mu g} (12\mu g L) = \frac{5 \times 12}{18} L = \frac{60}{18} L = \frac{10}{3} L$.

Let's recheck the assumption $v_a' = v$ and $v_{bc}' = v/2$. Consider the energy dissipated due to friction: $W_{friction} = -\mu mg |\Delta x_{rel}| = -\mu mg L$. Change in kinetic energy: $\Delta K = \frac{3}{2} m v_{final}^2 - (\frac{1}{2} m v_a'^2 + m v_{bc}'^2) = \frac{3}{2} m (\frac{2v}{3})^2 - (\frac{1}{2} m v^2 + m (v/2)^2) = \frac{2}{3} m v^2 - (\frac{1}{2} m v^2 + \frac{1}{4} m v^2) = \frac{2}{3} m v^2 - \frac{3}{4} m v^2 = (\frac{2}{3} - \frac{3}{4}) m v^2 = (\frac{8-9}{12}) m v^2 = -\frac{1}{12} m v^2$. So, $-\mu mg L = -\frac{1}{12} m v^2$, which means $\mu g L = \frac{1}{12} v^2$, or $v^2 = 12\mu g L$. This is consistent with our previous finding from relative displacement.

The displacement of board (a) is $\Delta x = \frac{5v^2}{18\mu g}$. Substitute $v^2 = 12\mu g L$: $\Delta x = \frac{5}{18\mu g} (12\mu g L) = \frac{5 \times 12}{18} L = \frac{60}{18} L = \frac{10}{3} L$.

The problem states that the displacement $\Delta x$ of board (a) is $\frac{\alpha L}{21}$. So, $\frac{10}{3} L = \frac{\alpha L}{21}$. $\frac{10}{3} = \frac{\alpha}{21}$ $\alpha = \frac{10}{3} \times 21 = 10 \times 7 = 70$.

The value of $\alpha$ is 70.

Let's double check the understanding of the problem. "Board -(a) stops moving relative to board-(b) and (c) at the moment it is entirely located on top of board-(c)." Initially, (a) is entirely on top of (b). When (a) is entirely on top of (c), and relative motion stops, it means (a) has moved relative to (b+c) by a distance equal to the length of board (c), which is L. This relative displacement is the distance between the initial position of the front/back edge of (a) relative to the front/back edge of (b+c) and the final position. Assuming that initially the front edge of (a) is aligned with the front edge of (b), and after sliding, the front edge of (a) is aligned with the front edge of (c) (or the coupled (b+c)), and (a) is entirely on top of (c). Since the length of (a) is L and the length of (c) is L, for (a) to be entirely on top of (c), the center of (a) must be within a distance L/2 from the center of (c). If initially (a) is on top of (b), let's say the center of (a) and (b) are aligned. After the collision, (b) and (c) are coupled. Let's assume the centers of (b) and (c) are initially separated by some distance. When (a) is entirely on top of (c), the relative displacement of the center of (a) with respect to the center of (b+c) is L.

Let's consider the relative displacement of the front edge of board (a) with respect to the front edge of the coupled board (b+c). Initially, let the front edge of (a) and (b) be at the same position. Let the front edge of (c) be at some distance to the right. After the collision, (b) and (c) are coupled. Let's assume the collision happens when the front edge of (b) meets the front edge of (c). Then, immediately after the collision, the front edge of (b+c) is at this position. If (a) was initially entirely on top of (b), its front edge is aligned with (b). When (a) is entirely on top of (c), its front edge is aligned with the front edge of (c) (or (b+c)). The relative displacement of the front edge of (a) with respect to the front edge of (b+c) is the distance slid by (a) relative to (b+c). When (a) is entirely on top of (c), it has moved a distance L relative to (b+c).

So, the relative displacement $|\Delta x_{rel}| = L$. Our calculation gave $|\Delta x_{rel}| = \frac{v^2}{12\mu g}$. So, $L = \frac{v^2}{12\mu g}$, which gives $v^2 = 12\mu g L$. The displacement of board (a) is $\Delta x = \frac{5v^2}{18\mu g}$. Substituting $v^2 = 12\mu g L$, we get $\Delta x = \frac{5}{18\mu g} (12\mu g L) = \frac{60}{18} L = \frac{10}{3} L$. We are given $\Delta x = \frac{\alpha L}{21}$. $\frac{10}{3} L = \frac{\alpha L}{21}$ $\frac{10}{3} = \frac{\alpha}{21}$ $\alpha = \frac{10}{3} \times 21 = 10 \times 7 = 70$.

The value of $\alpha$ is 70.