Question

A sphere of mass 10 kg is placed in between an inclined plane and a vertical frictionless wall as shown in the figure. The coefficient of friction between the inclined plane and the sphere 0.5. Determine the frictional force between the sphere and the inclined plane.

Answer 1

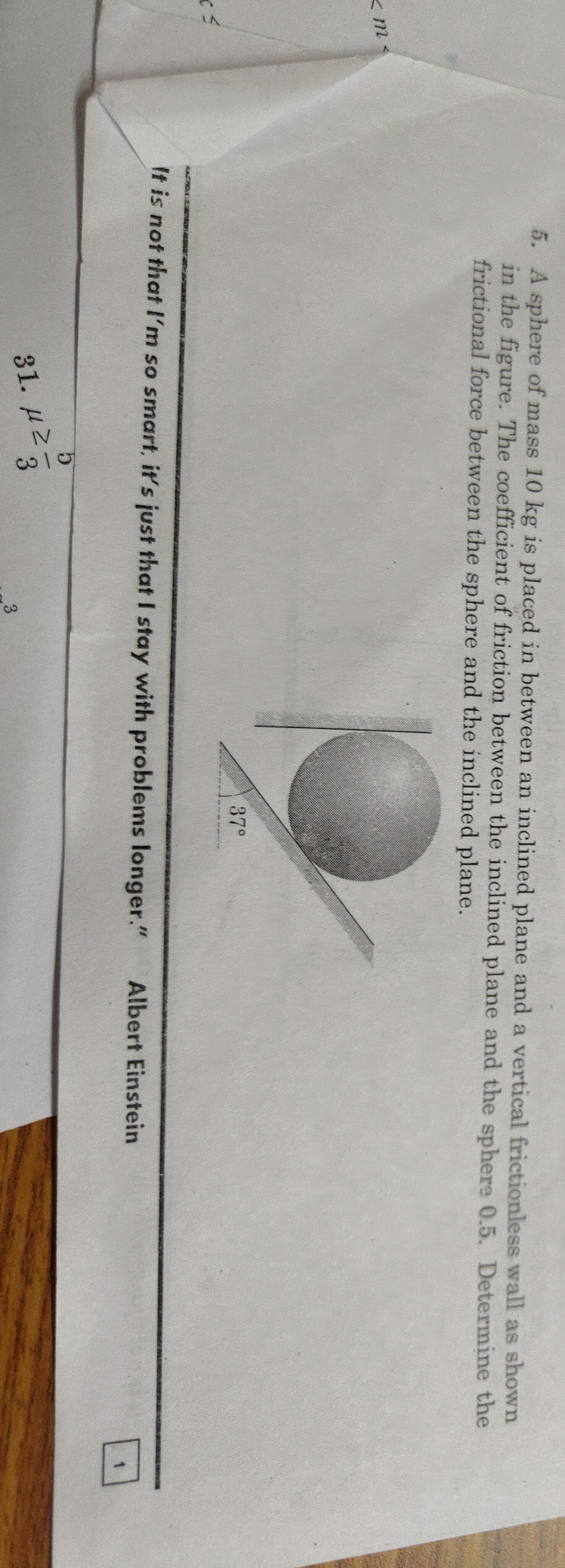
The frictional force between the sphere and the inclined plane is $\frac{500}{11} \text{ N}$.

Answer 2

Here's a detailed explanation of how to determine the frictional force:

1. Identify forces: Weight ($mg$), normal forces ($N_1$ from the plane, $N_2$ from the wall), and static friction ($f_s$).

2. Set up equilibrium equations in horizontal and vertical directions:

   • $\sum F_x = 0 \Rightarrow N_1 \sin 37^\circ + f_s \cos 37^\circ - N_2 = 0$
   • $\sum F_y = 0 \Rightarrow N_1 \cos 37^\circ + f_s \sin 37^\circ - mg = 0$

3. Substitute values ($m = 10 \text{ kg}$, $g = 10 \text{ m/s}^2$, $\sin 37^\circ \approx 0.6$, $\cos 37^\circ \approx 0.8$):

   • $0.6 N_1 + 0.8 f_s - N_2 = 0$
   • $0.8 N_1 + 0.6 f_s - 100 = 0$

4. Recognize the system is indeterminate (3 unknowns: $N_1, N_2, f_s$; and 2 equations). Assume the sphere is on the verge of slipping, which is a common interpretation for "determine the frictional force" when $\mu$ is given. This provides the third equation: $f_s = \mu N_1 = 0.5 N_1$.

5. Substitute $f_s = 0.5 N_1$ into the vertical equilibrium equation:

   $0.8 N_1 + 0.6 (0.5 N_1) = 100$ $0.8 N_1 + 0.3 N_1 = 100$ $1.1 N_1 = 100$ $N_1 = \frac{100}{1.1} = \frac{1000}{11} \text{ N}$

6. Calculate $f_s$:

   $f_s = 0.5 N_1 = 0.5 \times \frac{1000}{11} = \frac{500}{11} \text{ N}$

Therefore, the frictional force between the sphere and the inclined plane is $\frac{500}{11} \text{ N}$.