Question

A small Block A is released from the top of an incline plane at height of h=512 m. All the surface is frictionless. The block collides with the ground inelastically but does not stick to it. After collision with the spring, it returns back and collides with the incline inelastically but again does not stick to it. Find the maximum height (in m) from the ground attained by block A when it climbs up the incline.

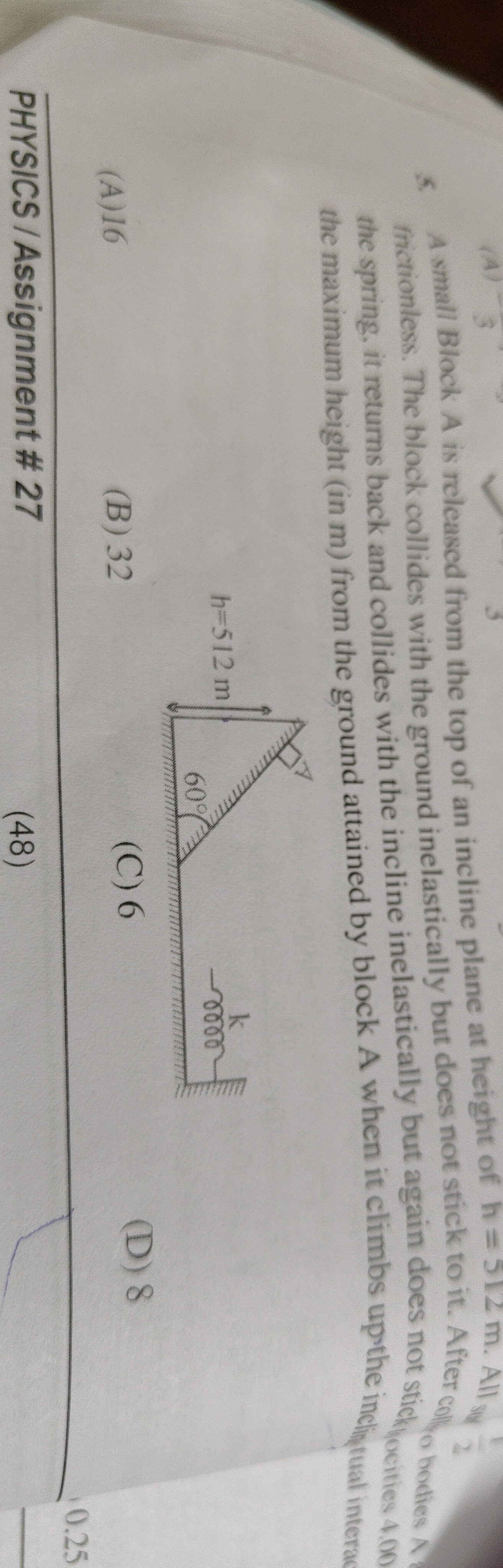
• A. 16
• B. 32
• C. 6
• D. 8

Answer 1

Answer: (B)

32

Answer 2

The problem involves energy conservation and inelastic collisions.

1. Initial State:
A block of mass m is released from rest at a height h = 512 m on a frictionless incline.
Its initial potential energy is PE_initial = mgh.
When it reaches the bottom of the incline, all this potential energy is converted into kinetic energy:
KE_before_1st_collision = mgh.

2. First Inelastic Collision (with the ground/spring):
The block collides with the ground inelastically. In an inelastic collision, kinetic energy is lost. The relationship between kinetic energy before and after a collision with a stationary object is given by the coefficient of restitution e.
If v is the speed before the collision and v' is the speed after, then v' = e * v.
Consequently, the kinetic energy after the collision (KE') is related to the kinetic energy before (KE) by:
KE' = (1/2)m(v')^2 = (1/2)m(ev)^2 = e^2 * (1/2)mv^2 = e^2 * KE.
The value 0.25 given on the page is a strong hint for e^2. Let's assume e^2 = 0.25. This implies e = 0.5.

So, after the first collision, the kinetic energy of the block is:
KE_after_1st_collision = e^2 * KE_before_1st_collision = 0.25 * mgh.

3. Climbing after the First Collision:
This kinetic energy is converted back into potential energy as the block climbs up the frictionless incline. Let the maximum height attained be h_1.
mgh_1 = KE_after_1st_collision
mgh_1 = 0.25 * mgh
h_1 = 0.25 * h
h_1 = (1/4) * 512 m = 128 m.
The block reaches h_1 and then slides back down.

4. Before the Second Inelastic Collision:
As the block slides down from h_1, its potential energy mgh_1 is converted back into kinetic energy at the bottom of the incline.
KE_before_2nd_collision = mgh_1 = 0.25 * mgh.

5. Second Inelastic Collision (with the incline):
The block collides with the incline inelastically again. Assuming the same coefficient of restitution e (and thus e^2 = 0.25), the kinetic energy after this collision will be:
KE_after_2nd_collision = e^2 * KE_before_2nd_collision
KE_after_2nd_collision = 0.25 * (0.25 * mgh)
KE_after_2nd_collision = (0.25)^2 * mgh = (1/4)^2 * mgh = (1/16) * mgh.

6. Final Climb and Maximum Height:
This final kinetic energy is converted into potential energy as the block climbs up the incline to its maximum height h_f.
mgh_f = KE_after_2nd_collision
mgh_f = (1/16) * mgh
h_f = (1/16) * h
h_f = (1/16) * 512 m
h_f = 32 m.

The maximum height attained by block A from the ground is 32 m.