Question

A rod of length l is translating with velocity v making an angle $\theta$ with the length. Find potential difference across the rod.

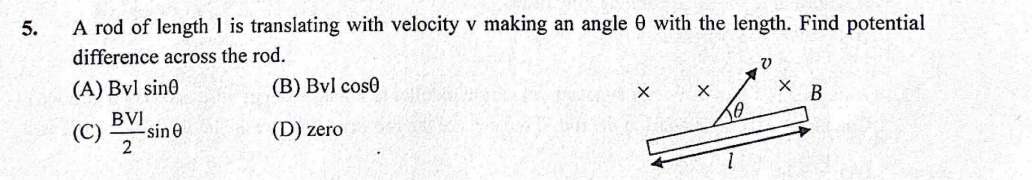
• A. Bvl sin$\theta$
• B. Bvl cos$\theta$
• C. $\frac{Bvl}{2}$sin$\theta$
• D. zero

Answer 1

Answer: (A)

Bvl sin$\theta$

Answer 2

The potential difference across the rod is given by the motional EMF, $\mathcal{E} = (\vec{v} \times \vec{B}) \cdot \vec{l}$.

Given that the magnetic field $\vec{B}$ is perpendicular to the plane containing the velocity $\vec{v}$ and the length of the rod $\vec{l}$, it means $\vec{B}$ is perpendicular to both $\vec{v}$ and $\vec{l}$.

The component of velocity perpendicular to the rod is $v \sin\theta$. This component is also perpendicular to the magnetic field $\vec{B}$.

Therefore, the induced EMF is given by the product of the magnetic field strength, the length of the rod, and the component of velocity perpendicular to the rod and magnetic field:

$\mathcal{E} = B \cdot l \cdot (v \sin\theta) = Bvl \sin\theta$.