Question

A player tosses 2 fair coins. He wins ₹ 5 if 2 heads appear, ₹ 21 if 1 head appears a) if no heads appear, then the variance of his winning amount is

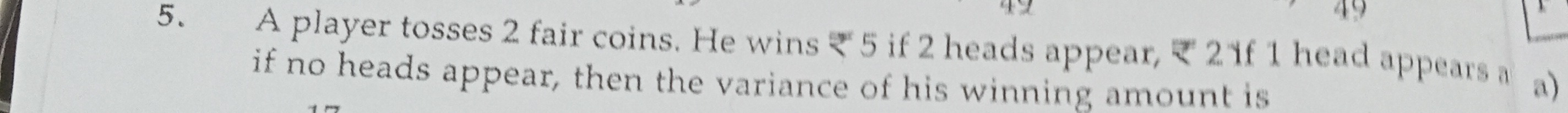
• A. 1419/16

Answer 1

Answer: (A)

1419/16

Answer 2

We are given a two‐coin toss game where the winning amounts are:

• ₹5 if 2 heads appear,
• ₹21 if 1 head appears, and
• ₹0 if no heads appear.

Let the random variable $X$ denote the winning amount. The probabilities are:

$$P(X=5)=\frac{1}{4},\quad P(X=21)=\frac{1}{2},\quad P(X=0)=\frac{1}{4}.$$

Step 1. Compute the expected value $E[X]$:

$$E[X] = 5\left(\frac{1}{4}\right) + 21\left(\frac{1}{2}\right) + 0\left(\frac{1}{4}\right) = \frac{5}{4} + \frac{21}{2}.$$

To add, convert to a common denominator:

$$\frac{5}{4} + \frac{21}{2} = \frac{5}{4} + \frac{42}{4} = \frac{47}{4}.$$

Step 2. Compute $E[X^2]$:

$$E[X^2] = 5^2\left(\frac{1}{4}\right) + 21^2\left(\frac{1}{2}\right) + 0^2\left(\frac{1}{4}\right) = \frac{25}{4} + \frac{441}{2}.$$

Convert the second term:

$$\frac{441}{2} = \frac{882}{4}, \quad \text{thus,} \quad E[X^2] = \frac{25}{4} + \frac{882}{4} = \frac{907}{4}.$$

Step 3. Compute the variance $\mathrm{Var}(X)$:

$$\mathrm{Var}(X) = E[X^2] - \bigl(E[X]\bigr)^2 = \frac{907}{4} - \left(\frac{47}{4}\right)^2.$$

Calculate $\left(\frac{47}{4}\right)^2$:

$$\left(\frac{47}{4}\right)^2 = \frac{2209}{16}.$$

Write $E[X^2]$ with denominator 16:

$$\frac{907}{4} = \frac{907 \times 4}{16} = \frac{3628}{16}.$$

Thus,

$$\mathrm{Var}(X) = \frac{3628}{16} - \frac{2209}{16} = \frac{1419}{16}.$$

Final Answer:

The variance of his winning amount is $\displaystyle \frac{1419}{16}$ (approximately ₹88.69).

---

Explanation (minimal core):

• Tossing 2 coins gives probabilities: $P(2H)=\frac{1}{4}$, $P(1H)=\frac{1}{2}$, $P(0H)=\frac{1}{4}$.
• Compute $E[X]=\frac{47}{4}$.
• Compute $E[X^2]=\frac{907}{4}$.
• Then, $\mathrm{Var}(X)=\frac{907}{4} - \left(\frac{47}{4}\right)^2 = \frac{1419}{16}$.