Question

A player tosses 2 fair coins. He wins ₹ 5 if 2 heads appear, ₹ 21f 1 head appears a) if no heads appear, then the variance of his winning amount is

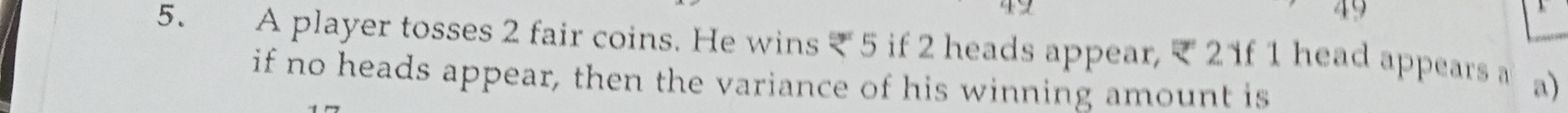
Answer 1

$\displaystyle \frac{9}{4}$

Answer 2

Let the random variable $X$ denote the winning amount. The outcomes when tossing 2 fair coins (each outcome having probability $\frac{1}{4}$) are:

• 2 heads (HH): $X = 5$
• 1 head (HT or TH): $X = 2$
• No heads (TT): $X = 1$

Step 1: Compute the Expected Value

$$E(X) = \frac{1}{4}(5) + \frac{2}{4}(2) + \frac{1}{4}(1) = \frac{5 + 4 + 1}{4} = \frac{10}{4} = 2.5$$

Step 2: Compute the Expected Value of $X^2$

$$E(X^2) = \frac{1}{4}(5^2) + \frac{2}{4}(2^2) + \frac{1}{4}(1^2) = \frac{25 + 8 + 1}{4} = \frac{34}{4} = 8.5$$

Step 3: Calculate the Variance

$$\text{Var}(X) = E(X^2) - [E(X)]^2 = 8.5 - (2.5)^2 = 8.5 - 6.25 = 2.25 = \frac{9}{4}$$