Question

A plank of mass M=4kg is symmetrically placed over two identical cylinders of radius R and identical mass M as shown in the following figure. A vertical spring of natural length R and spring constant k = 700 × $\pi^2$ N/m is connecting the center of the plank with the ground. All surfaces are rough and there is no slippage anywhere. The plank is displaced horizontally by a very small length A from the mean position and released. Choose the correct option(s).

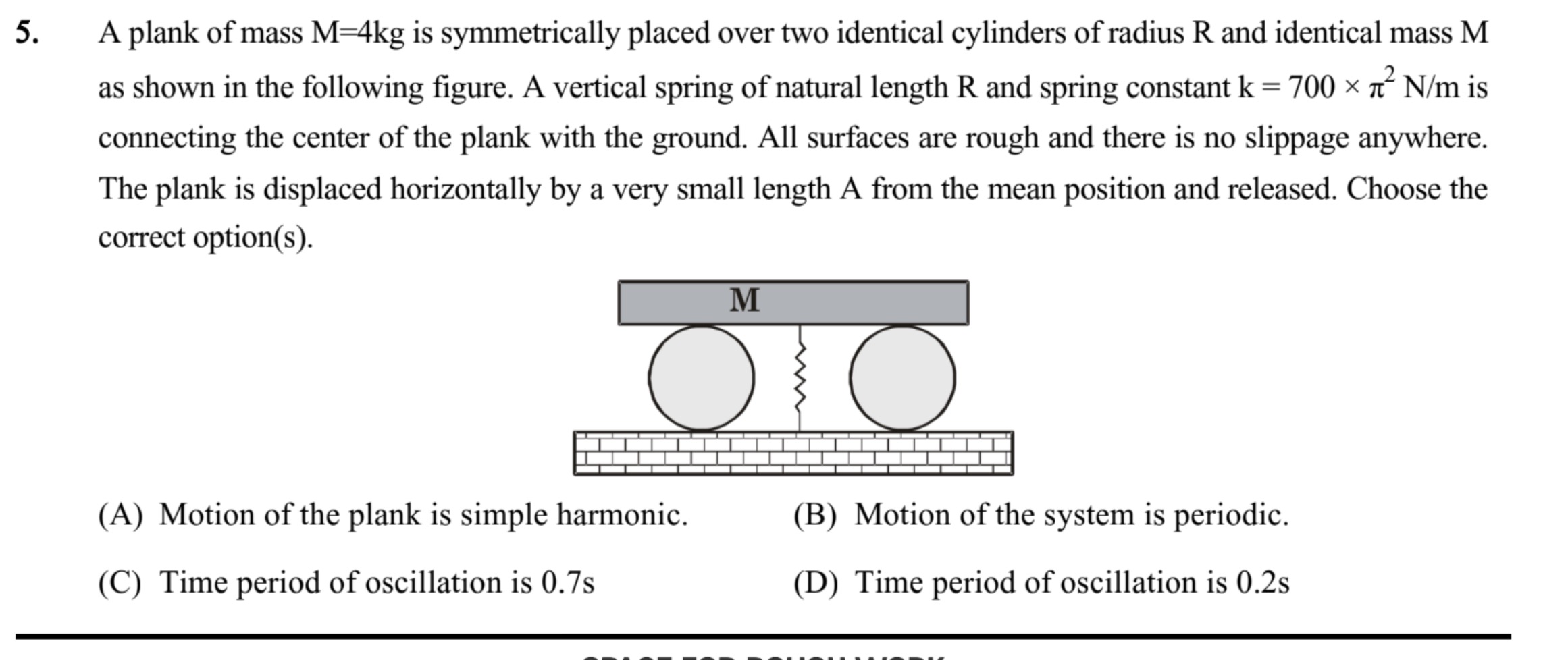
• A. Motion of the plank is simple harmonic.
• B. Motion of the system is periodic.
• C. Time period of oscillation is 0.7s
• D. Time period of oscillation is 0.2s

Answer 1

Answer: (A), (B), (D)

Options (A), (B) and (D).

Answer 2

We will show that when the plank is given a small horizontal displacement the following occurs. In equilibrium the plank rests on top of the two identical cylinders (each of mass M and radius R) and is supported vertically by a “vertical” spring whose natural length is R. (In fact the plank’s underside is in tangential contact with the tops of the cylinders, whose centers lie a distance R above the horizontal floor; so the plank is at height 2R and the spring is extended by R at equilibrium.) Now, if you displace the plank laterally by a small amount x, the top‐end of the spring moves from (0,2R) to (x,2R). Although the spring “remains vertical” (its line of action fixed vertically because its lower end is fixed) the top is now off the vertical line from the lower end and the spring force has a nonzero horizontal component. (A standard geometry shows that for small x the horizontal component is)

$F_x \simeq k(R)(x/(2R)) = (k/2)x$

(Notice that the extra extension of the spring—i.e. the change in its length—is only a second–order small quantity; the first–order effect comes entirely from the “leaning” of the spring.)

Since the spring is attached only to the plank the net horizontal force on the plank is

$-(k/2)x$.

If one further shows (by a careful analysis of the no–slip conditions at the two contacts – the cylinders “roll” but their centers remain essentially fixed by the rough floor) that the cylinder “inertial corrections” do not affect the leading linear term, then the equation of motion for the horizontal displacement of the plank is

$M \ddot{x} + (k/2)x = 0$

with M = 4 kg. Thus the motion of the plank is simple‐harmonic with

$\omega = \sqrt{k/(2M)}$, T = $2\pi\sqrt{2M/k}$.

With k = 700π², one finds

T = $2\pi\sqrt{2×4/(700\pi²)}$ = $2\pi\sqrt{8/(700\pi²)}$ = $2\pi/(\pi) \sqrt{8/700}$ = $2 \sqrt{8/700}$ ≈ $2 \sqrt{0.01143}$ ≈ 2 (0.107) ≈ 0.214 s.

Thus the time period is about 0.2 s. (Also the whole “system” – plank plus the (rolling) cylinders – executes periodic motion.)

So the correct statements are:

(A) Motion of the plank is simple harmonic.

(B) Motion of the system is periodic.

(D) Time period of oscillation is 0.2 s.

Option (C) is not correct.

Explanation (very brief):

1. When the plank is shifted horizontally by a small x the spring (of constant k) now “leans”, so its horizontal component is ≈ (k/2)x.

2. The horizontal equation of motion for mass M becomes M x¨ + (k/2)x = 0, i.e. SHM.

3. Hence, T = $2\pi\sqrt{2M/k}$ ≈ 0.2 s.

4. Thus the overall system oscillates periodically.