Question

A particle is projected horizontally at a speed 5 m. $s^{-1}$ along a smooth inclined plane. The inclined piane is inclined at 30° with the horizontal. Find the radius of curvature (in m) followed by the particle 1s after the particle is projected, [g = 10 m. $s^{-2}$]

Answer 1

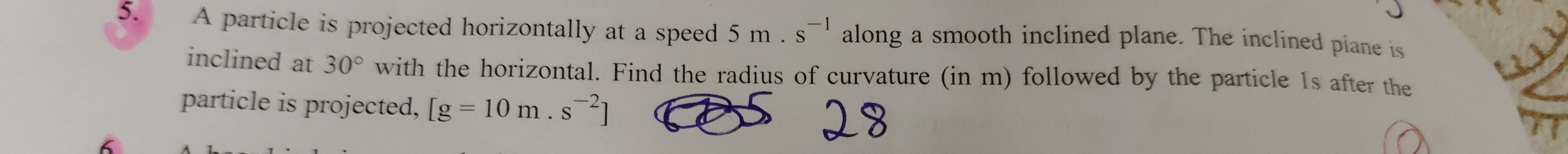
10√2

Answer 2

The problem describes the motion of a particle projected horizontally on a smooth inclined plane. This is a case of projectile motion on an inclined plane.

1. Define Coordinate System and Acceleration: Let's set up a coordinate system on the inclined plane.

• The x-axis is chosen along the initial projection direction (horizontal on the plane).
• The y-axis is chosen perpendicular to the x-axis, pointing down the incline.

The only force acting on the particle along the plane is the component of gravity parallel to the plane. The acceleration due to gravity g acts vertically downwards. The angle of inclination is θ = 30°. The component of g parallel to the inclined plane is a_y = g sin(θ). Given g = 10 m/s^2 and θ = 30°: a_y = 10 * sin(30°) = 10 * (1/2) = 5 m/s^2. Since the projection is horizontal on the plane, there is no acceleration component along the x-axis (a_x = 0). So, the acceleration vector a = (0, 5) m/s^2.

2. Initial Velocity: The particle is projected horizontally at a speed of 5 m/s along the x-axis. Initial velocity components: u_x = 5 m/s u_y = 0 m/s Initial velocity vector u = (5, 0) m/s.

3. Velocity at t = 1s: Using kinematic equations for constant acceleration: v_x(t) = u_x + a_x * t = 5 + 0 * t = 5 m/s v_y(t) = u_y + a_y * t = 0 + 5 * t = 5t m/s At t = 1s: v_x = 5 m/s v_y = 5 * 1 = 5 m/s The velocity vector at t = 1s is v = (5, 5) m/s. The magnitude of the velocity |v| = sqrt(v_x^2 + v_y^2) = sqrt(5^2 + 5^2) = sqrt(25 + 25) = sqrt(50) = 5 * sqrt(2) m/s.

4. Radius of Curvature Formula: The radius of curvature R is given by the formula: R = |v|^2 / a_n where |v| is the magnitude of the velocity and a_n is the component of acceleration perpendicular to the velocity vector. The normal component of acceleration a_n can be found using a_n = |a| sin(α), where α is the angle between the velocity vector v and the acceleration vector a.

5. Calculate Angle α between v and a: The acceleration vector a = (0, 5) m/s^2. Its magnitude |a| = 5 m/s^2. The velocity vector v = (5, 5) m/s. Its magnitude |v| = 5 * sqrt(2) m/s. Using the dot product formula: v . a = |v| |a| cos(α) v . a = (5)(0) + (5)(5) = 25 25 = (5 * sqrt(2)) * 5 * cos(α) 25 = 25 * sqrt(2) * cos(α) cos(α) = 1 / sqrt(2) Therefore, α = 45°.

6. Calculate a_n: a_n = |a| sin(α) = 5 * sin(45°) = 5 * (1 / sqrt(2)) = 5 / sqrt(2) m/s^2.

7. Calculate Radius of Curvature R: R = |v|^2 / a_n R = (5 * sqrt(2))^2 / (5 / sqrt(2)) R = 50 / (5 / sqrt(2)) R = 50 * (sqrt(2) / 5) R = 10 * sqrt(2) m.

The radius of curvature followed by the particle 1s after projection is 10 * sqrt(2) m.