Question

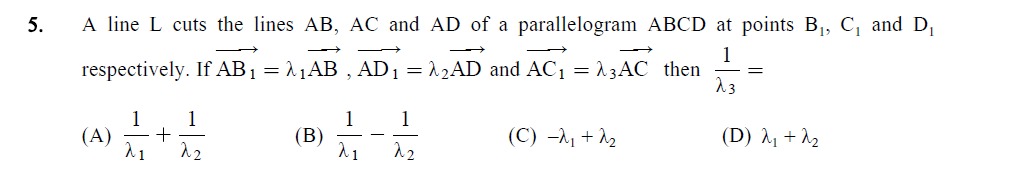
A line L cuts the lines AB, AC and AD of a parallelogram ABCD at points B₁, C₁ and D₁ respectively. If $\overrightarrow{AB_1} = \lambda_1\overrightarrow{AB}$, $\overrightarrow{AD_1} = \lambda_2\overrightarrow{AD}$ and $\overrightarrow{AC_1} = \lambda_3\overrightarrow{AC}$ then $\frac{1}{\lambda_3} =$

• A. $\frac{1}{\lambda_1} + \frac{1}{\lambda_2}$
• B. $\frac{1}{\lambda_1} - \frac{1}{\lambda_2}$
• C. $-\lambda_1 + \lambda_2$
• D. $\lambda_1 + \lambda_2$

Answer 1

Answer: (A)

$\frac{1}{\lambda_1} + \frac{1}{\lambda_2}$

Answer 2

Let $A$ be the origin, $B$ be represented by vector $\mathbf{b}$, and $D$ by $\mathbf{d}$. Then, in the parallelogram, $C = B + D = \mathbf{b} + \mathbf{d}$.

Given:

$$\overrightarrow{AB_1} = \lambda_1 \mathbf{b}, \quad \overrightarrow{AD_1} = \lambda_2 \mathbf{d}, \quad \overrightarrow{AC_1} = \lambda_3(\mathbf{b}+\mathbf{d}).$$

The line $L$ passes through points $B_1$ and $D_1$. Its parametric equation is:

$$\mathbf{r} = \lambda_1 \mathbf{b} + t\Big(\lambda_2 \mathbf{d} - \lambda_1 \mathbf{b}\Big) = \lambda_1(1-t)\mathbf{b} + \lambda_2 t\, \mathbf{d}.$$

Since point $C_1$ lies on $L$, we have:

$$\lambda_3 (\mathbf{b}+\mathbf{d}) = \lambda_1(1-t)\mathbf{b} + \lambda_2t\, \mathbf{d}.$$

Equate coefficients of $\mathbf{b}$ and $\mathbf{d}$:

$$\lambda_3 = \lambda_1(1-t) \quad \text{and} \quad \lambda_3 = \lambda_2t.$$

From the second equation:

$$t = \frac{\lambda_3}{\lambda_2}.$$

Substitute into the first equation:

$$\lambda_3 = \lambda_1\left(1-\frac{\lambda_3}{\lambda_2}\right) \implies \lambda_3 = \frac{\lambda_1(\lambda_2-\lambda_3)}{\lambda_2}.$$

Multiply through by $\lambda_2$:

$$\lambda_3\lambda_2 = \lambda_1(\lambda_2 - \lambda_3).$$

Rearrange:

$$\lambda_3\lambda_2 + \lambda_1\lambda_3 = \lambda_1\lambda_2,$$ $$\lambda_3(\lambda_1+\lambda_2)=\lambda_1\lambda_2.$$

Thus:

$$\lambda_3 = \frac{\lambda_1\lambda_2}{\lambda_1+\lambda_2},$$

and taking reciprocals,

$$\frac{1}{\lambda_3}=\frac{\lambda_1+\lambda_2}{\lambda_1\lambda_2} = \frac{1}{\lambda_1}+\frac{1}{\lambda_2}.$$