Question

A double ordinate of the curve $y^2 = 4px$ is of length $8p$; prove that the lines from the vertex to its two ends are at right angles.

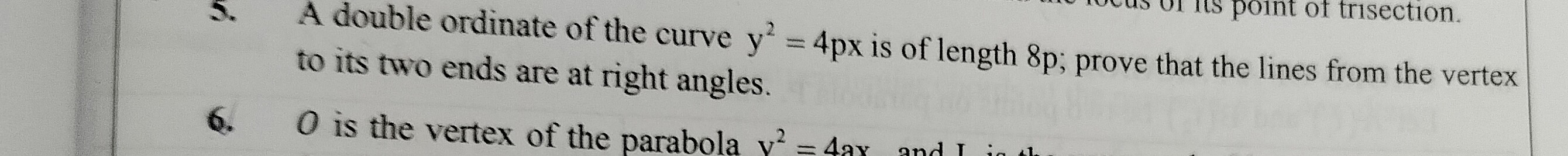
• A. The lines are at right angles.
• B. The lines are parallel.
• C. The lines are coincident.
• D. The lines are perpendicular bisectors of each other.

Answer 1

Answer: (A)

The lines are at right angles.

Answer 2

Let the parabola be $y^2 = 4px$. The vertex is O $(0,0)$. Let the endpoints of the double ordinate be P and Q. The parametric coordinates of a point on the parabola are $(pt^2, 2pt)$. Let P be $(pt^2, 2pt)$ and Q be $(pt^2, -2pt)$. The length of the double ordinate PQ is $|2pt - (-2pt)| = |4pt|$. Given that the length is $8p$, we have $|4pt| = 8p$. Assuming $p>0$, we get $4pt = 8p$, which implies $t=2$.

The slope of the line OP (from vertex $(0,0)$ to P $(pt^2, 2pt)$) is: $m_{OP} = \frac{2pt - 0}{pt^2 - 0} = \frac{2pt}{pt^2} = \frac{2}{t}$

The slope of the line OQ (from vertex $(0,0)$ to Q $(pt^2, -2pt)$) is: $m_{OQ} = \frac{-2pt - 0}{pt^2 - 0} = \frac{-2pt}{pt^2} = -\frac{2}{t}$

To prove that OP and OQ are at right angles, we check the product of their slopes: $m_{OP} \times m_{OQ} = \left(\frac{2}{t}\right) \times \left(-\frac{2}{t}\right) = -\frac{4}{t^2}$

Substituting the value $t=2$: $m_{OP} \times m_{OQ} = -\frac{4}{(2)^2} = -\frac{4}{4} = -1$

Since the product of the slopes is -1, the lines OP and OQ are at right angles.