Question
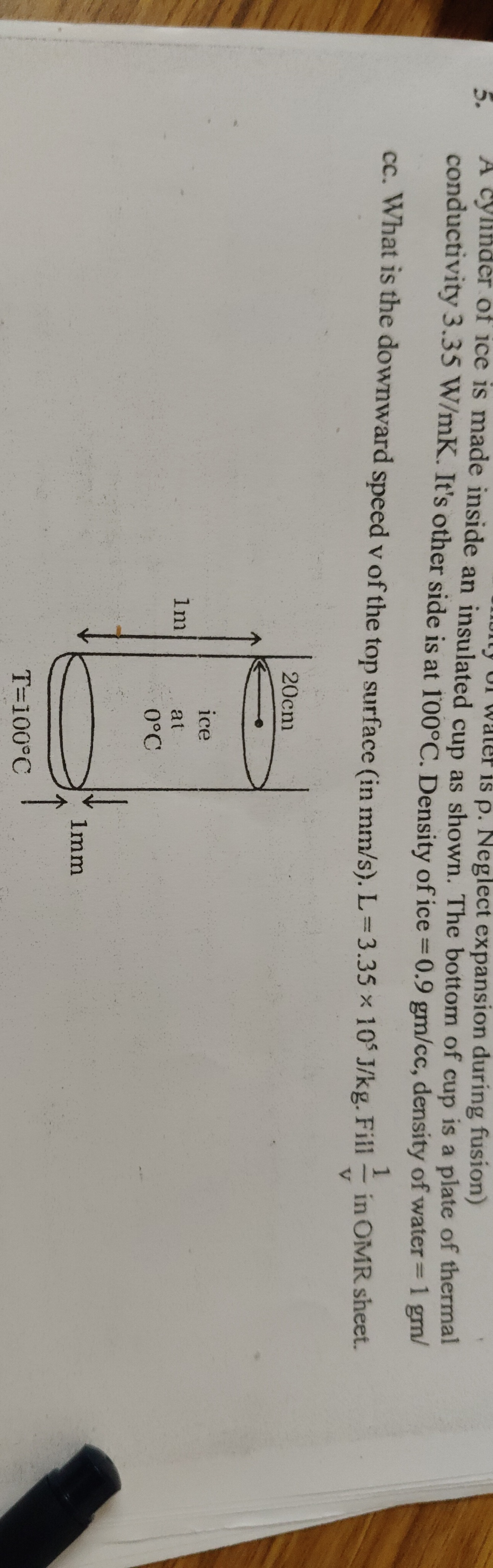
Question: A cylinder of ice is made inside an insulated cup as shown. The bottom of cup is a plate of thermal ...
A cylinder of ice is made inside an insulated cup as shown. The bottom of cup is a plate of thermal conductivity 3.35 W/mK. It's other side is at 100°C. Density of ice = 0.9 gm/cc, density of water = 1 gm/cc. What is the downward speed v of the top surface (in mm/s). L = 3.35 x 10⁵ J/kg.
10/9 mm/s
Solution
The rate of heat transfer through the bottom plate is calculated using Fourier's Law of conduction: tQ=kAΔxΔT. Given: k=3.35 W/mK A=πr2=π(0.1 m)2=0.01π m2 (radius r=20cm/2=10cm=0.1m) ΔT=100∘C−0∘C=100 K Δx=1 mm=0.001 m
tQ=(3.35 W/mK)×(0.01π m2)×0.001 m100 K=3.35×0.01π×100000 W=3350π W
This heat is used to melt the ice. The rate of mass melting (dm/dt) is given by tQ=dtdmL. dtdm=3.35×105 J/kg3350π J/s=3.35×1053.35×103π kg/s=100π kg/s
The rate of volume decrease of ice (dVice/dt) is dtdVice=ρicedm/dt. Density of ice ρice=0.9 gm/cc=0.9×103 kg/m3. dtdVice=0.9×103 kg/m3π/100 kg/s=90000π m3/s
The downward speed v of the top surface is related to the rate of volume decrease by dtdVice=Av. v=A1dtdVice=0.01π m21×90000π m3/s=0.01×900001 m/s=9001 m/s
Converting to mm/s: v=9001 m/s×1000 mm/m=9001000 mm/s=910 mm/s
