Question

A cubical container has 2 fixed vertical walls and two vertical walls can freely rotate about one of the horizontal edges. The right wall can rotate about upper edge and the left wall can rotate about the bottom edge. Water is filled upto the top and forces F₁ and F₂ (perpendicular to the walls) are applied to keep the walls at from opening as shown in figure. Given that the cube is at rest on a

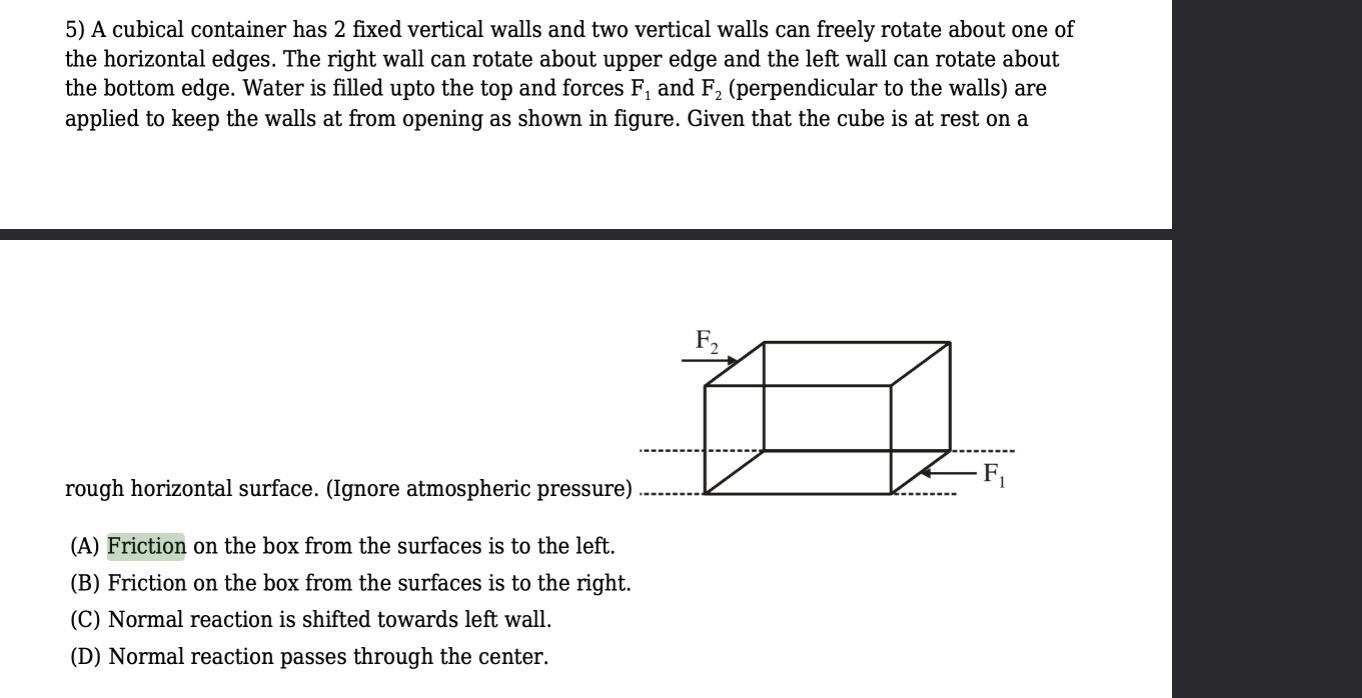
• A. Friction on the box from the surfaces is to the left.
• B. Friction on the box from the surfaces is to the right.
• C. Normal reaction is shifted towards left wall.
• D. Normal reaction passes through the center.

Answer 1

Answer: (A), (C)

Options (A) and (C)

Answer 2

1. Force Analysis:

• Two forces are applied:

  • $F_1$ at the bottom right (acting leftward)
  • $F_2$ at the top left (acting rightward)

• In order for the container to remain in translational equilibrium, the net horizontal force must be zero, so the floor must provide a friction force. Since typically the water pressure creates a higher moment from the top (where $F_2$ is applied) compared to the bottom (where $F_1$ is applied), we end up with $F_2 > F_1$.

• Thus, the net horizontal force (before the floor reaction) is rightward. To balance it, the friction force from the floor must act towards the left.

2. Moment Equilibrium and Normal Reaction:

• The couple produced by the forces $F_1$ and $F_2$ tends to rotate the body.
• To counteract this, the line of action of the normal reaction from the floor shifts towards the side with the larger moment (i.e. the left wall), thus creating a counter moment.
• Hence, the normal reaction is shifted towards the left wall rather than acting through the center.