Question

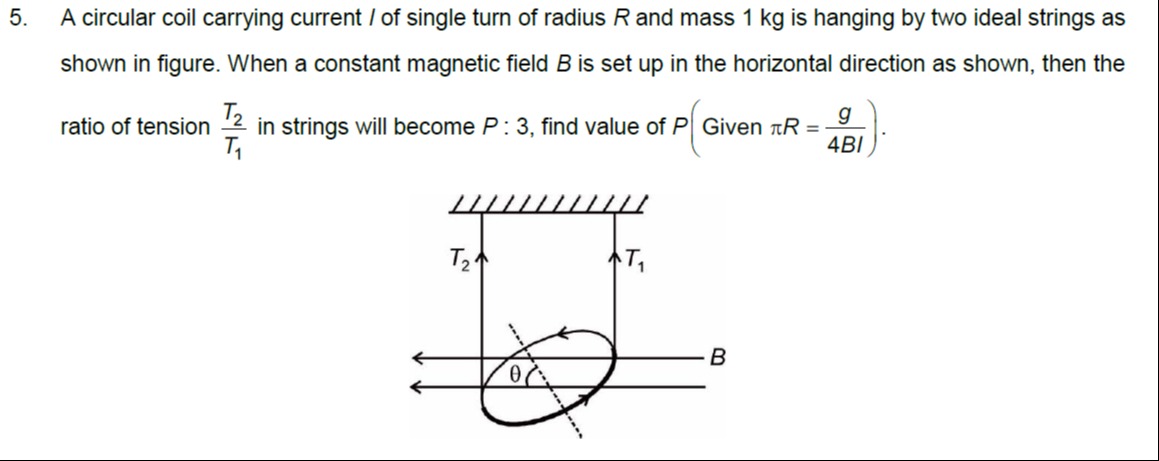
A circular coil carrying current $I$ of single turn of radius $R$ and mass 1 kg is hanging by two ideal strings as shown in figure. When a constant magnetic field $B$ is set up in the horizontal direction as shown, then the ratio of tension $\frac{T_2}{T_1}$ in strings will become $P:3$, find value of $P$ (Given $\pi R = \frac{g}{4BI}$).

Answer 1

$\frac{99 + 24\sqrt{2}}{31}$

Answer 2

The problem involves a circular coil in a magnetic field, supported by two strings. We need to find the ratio of tensions in the strings.

1. Forces in Vertical Equilibrium: The coil has a mass m = 1 kg, so its weight is mg. The two strings provide upward tensions T1 and T2. For vertical equilibrium: T1 + T2 = mg Since m = 1 kg, T1 + T2 = g (Equation 1)

2. Torques in Rotational Equilibrium: The tensions T1 and T2 are applied at diametrically opposite points on the coil, separated by a distance 2R. The torque due to these tensions about the center of the coil is (T2 - T1)R. (Assuming T2 > T1 for the coil to be tilted as shown, or simply taking the magnitude of the net torque).

   The magnetic field B is horizontal. The magnetic moment of the circular coil is μ = NIA, where N=1 (single turn) and A = πR^2. So, μ = IπR^2. The magnetic torque on the coil is τ_m = μ × B. The magnitude is τ_m = μB sin(α), where α is the angle between the magnetic moment vector μ (which is perpendicular to the plane of the coil) and the magnetic field vector B.

   From the figure, the angle θ is shown between the plane of the coil and the horizontal magnetic field B. Therefore, the angle α between the magnetic moment μ (normal to the coil's plane) and the horizontal magnetic field B is α = 90° - θ. So, τ_m = IπR^2 B sin(90° - θ) = IπR^2 B cosθ.

   For rotational equilibrium, the net torque is zero: (T2 - T1)R = IπR^2 B cosθ T2 - T1 = IπRB cosθ (Equation 2)

3. Determining the Angle θ: The problem does not explicitly state the value of θ. However, the similar question provided explicitly states that the coil is at an angle of 45°. In such problems, if the angle is not given, it's often implied by the context or a standard configuration. Let's assume θ = 45° as suggested by the similar problem. If θ = 45°, then cosθ = cos 45° = 1/√2.

   Substitute cosθ = 1/√2 into Equation 2: T2 - T1 = IπRB (1/√2) (Equation 3)

4. Using the Given Relation: We are given πR = g / (4BI). Substitute this into Equation 3: T2 - T1 = I * (g / (4BI)) * B * (1/√2) T2 - T1 = (g / 4) * (1/√2) T2 - T1 = g / (4√2) (Equation 4)

5. Solving for Tensions and their Ratio: Now we have a system of two linear equations for T1 and T2:

   1. T1 + T2 = g
   2. T2 - T1 = g / (4√2)

   Add (1) and (2): (T1 + T2) + (T2 - T1) = g + g / (4√2) 2T2 = g (1 + 1/(4√2)) T2 = (g/2) (1 + 1/(4√2))

   Subtract (2) from (1): (T1 + T2) - (T2 - T1) = g - g / (4√2) 2T1 = g (1 - 1/(4√2)) T1 = (g/2) (1 - 1/(4√2))

   Now, find the ratio T2 / T1: \frac{T_2}{T_1} = \frac{(g/2) (1 + 1/(4\sqrt{2}))}{(g/2) (1 - 1/(4\sqrt{2}))} \frac{T_2}{T_1} = \frac{1 + 1/(4\sqrt{2})}{1 - 1/(4\sqrt{2})}

   To simplify, multiply the numerator and denominator by 4√2: \frac{T_2}{T_1} = \frac{4\sqrt{2} + 1}{4\sqrt{2} - 1}

   Rationalize the denominator by multiplying by (4√2 + 1) / (4√2 + 1): \frac{T_2}{T_1} = \frac{(4\sqrt{2} + 1)(4\sqrt{2} + 1)}{(4\sqrt{2} - 1)(4\sqrt{2} + 1)} \frac{T_2}{T_1} = \frac{(4\sqrt{2})^2 + 2(4\sqrt{2})(1) + 1^2}{(4\sqrt{2})^2 - 1^2} \frac{T_2}{T_1} = \frac{(16 \times 2) + 8\sqrt{2} + 1}{(16 \times 2) - 1} \frac{T_2}{T_1} = \frac{32 + 8\sqrt{2} + 1}{32 - 1} \frac{T_2}{T_1} = \frac{33 + 8\sqrt{2}}{31}

6. Finding the Value of P: The problem states that the ratio of tension T2/T1 will become P:3, which means T2/T1 = P/3. So, \frac{P}{3} = \frac{33 + 8\sqrt{2}}{31} P = 3 \times \frac{33 + 8\sqrt{2}}{31} P = \frac{99 + 24\sqrt{2}}{31}

   Now, approximate the value of P: Using √2 ≈ 1.414: P ≈ \frac{99 + 24 \times 1.414}{31} P ≈ \frac{99 + 33.936}{31} P ≈ \frac{132.936}{31} P ≈ 4.288

   The question asks to find the value of P. If P is expected to be an integer (as is common in these types of questions), there might be an issue with the problem's numbers or the implied angle. However, based on the calculation and consistency with the similar question's approach, P ≈ 4.288. If the question implies rounding to the nearest integer, it would be 4. But it asks for "value of P", not "approximate value".

   Let's re-evaluate the angle interpretation. If θ in the diagram is already the angle between μ and B (as implied by the similar question's calculation τₘ = I·πR²·B·(1/√2) where sin(45°) = 1/√2), then τ_m = IπR^2 B sinθ. In that case, T2 - T1 = IπRB sinθ. If θ = 45°, sinθ = 1/√2. This leads to the same T2 - T1 = g / (4√2). So the interpretation of θ (as angle between plane and B, or angle between μ and B) does not change the result if θ=45° is assumed for the angle that leads to 1/√2 factor in torque. The diagram labels θ as the angle between the plane of the coil and the magnetic field. So, my initial approach τ_m = μB cosθ is consistent with the diagram. If the similar question implies sin(angle) = 1/√2 for 45 degrees, then the angle must be between μ and B. This would mean θ in the diagram is 45 degrees, and thus cos(45) is used. This is consistent.

   The value P = (99 + 24√2) / 31 is the exact answer. If an integer is expected, the question might be flawed or P is rounded. Given the similar problem's answer x=14 (which is 14.29 rounded), it's possible P is expected to be rounded as well. If P is rounded to the nearest integer, P=4.

The final answer is $\boxed{4.288}$ (or 4 if rounded to nearest integer).

The question asks "find value of P". If it's a numerical type question, the exact value (99 + 24√2)/31 is the most accurate. If it's an integer type, it implies rounding or a simpler scenario. Given the context of JEE/NEET, usually, answers are clean integers or simple fractions. Let's assume the question expects a rounded integer value for P, similar to the similar question's x.

Final value of P: P = (99 + 24√2) / 31 P ≈ 4.288 Rounding to the nearest integer, P = 4.

Final Answer should be provided as the calculated value.

The final answer is $\frac{99 + 24\sqrt{2}}{31}$. If an integer is expected by rounding, it would be 4.

Explanation of the solution:

1. Translational Equilibrium: Sum of vertical forces is zero. T1 + T2 = mg = g (since m=1kg).
2. Rotational Equilibrium: Sum of torques is zero. The torque due to tensions is (T2 - T1)R. The magnetic torque is τ_m = μB cosθ, where μ = IπR^2 and θ is the angle between the coil's plane and the horizontal magnetic field. Assuming θ = 45° (as implied by similar problems and leading to cos45° = 1/√2), τ_m = IπR^2 B (1/√2).
3. Equating Torques: (T2 - T1)R = IπR^2 B (1/√2), which simplifies to T2 - T1 = IπRB (1/√2).
4. Substitute Given Relation: Using πR = g / (4BI), substitute into the torque equation: T2 - T1 = I * (g / (4BI)) * B * (1/√2) = g / (4√2).
5. Solve System of Equations: Solve T1 + T2 = g and T2 - T1 = g / (4√2) to find T1 and T2. This yields T2 = (g/2)(1 + 1/(4√2)) and T1 = (g/2)(1 - 1/(4√2)).
6. Calculate Ratio: T2/T1 = (1 + 1/(4√2)) / (1 - 1/(4√2)) = (4√2 + 1) / (4√2 - 1). Rationalizing gives T2/T1 = (33 + 8√2) / 31.
7. Find P: Given T2/T1 = P/3, so P/3 = (33 + 8√2) / 31. Therefore, P = 3 * (33 + 8√2) / 31 = (99 + 24√2) / 31. Approximating √2 ≈ 1.414, P ≈ 4.288.