Question

5. (a) $1 - \log 5 = \frac{1}{3} (\log\frac{1}{2} + \log x + \frac{1}{3} \log 5)$.

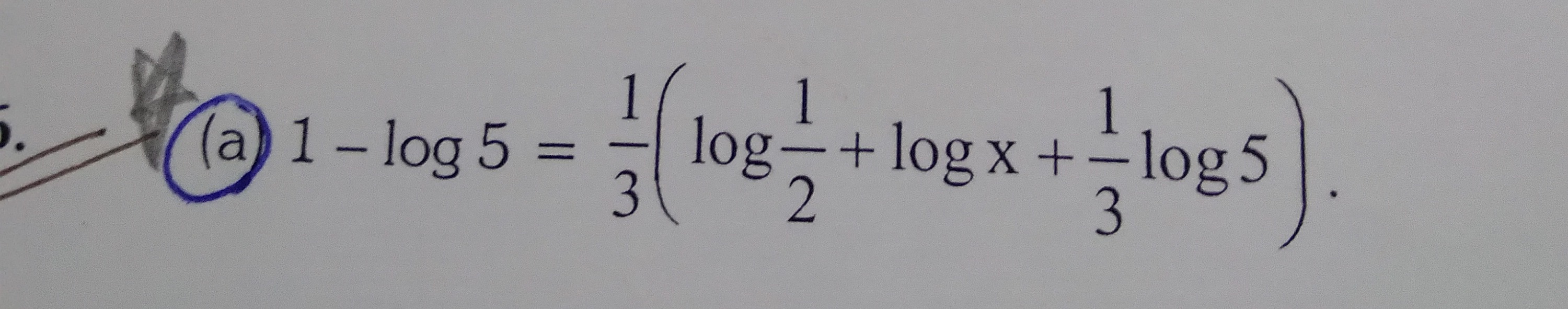
Answer 1

The value of $x$ is $\frac{16}{5^{1/3}}$ or $\frac{16}{\sqrt[3]{5}}$. This can also be written as $\frac{16 \sqrt[3]{25}}{5}$.

Answer 2

The equation is simplified by using logarithm properties. LHS: $1 - \log 5 = \log 10 - \log 5 = \log\left(\frac{10}{5}\right) = \log 2$. RHS: $\frac{1}{3} (\log\frac{1}{2} + \log x + \frac{1}{3} \log 5)$. Using $n \log a = \log(a^n)$: $\frac{1}{3} \log 5 = \log(5^{1/3})$. RHS = $\frac{1}{3} (\log\frac{1}{2} + \log x + \log(5^{1/3}))$. Using $\log a + \log b + \log c = \log(abc)$: RHS = $\frac{1}{3} \log\left(\frac{1}{2} \cdot x \cdot 5^{1/3}\right) = \frac{1}{3} \log\left(\frac{x \cdot 5^{1/3}}{2}\right)$. Equating LHS and RHS: $\log 2 = \frac{1}{3} \log\left(\frac{x \cdot 5^{1/3}}{2}\right)$. Multiply by 3: $3 \log 2 = \log\left(\frac{x \cdot 5^{1/3}}{2}\right)$. Using $n \log a = \log(a^n)$: $\log 2^3 = \log\left(\frac{x \cdot 5^{1/3}}{2}\right)$. $\log 8 = \log\left(\frac{x \cdot 5^{1/3}}{2}\right)$. Since $\log A = \log B \implies A = B$: $8 = \frac{x \cdot 5^{1/3}}{2}$. Multiply by 2: $16 = x \cdot 5^{1/3}$. Solve for $x$: $x = \frac{16}{5^{1/3}}$. This can also be written as $x = \frac{16}{\sqrt[3]{5}}$. To rationalize the denominator, multiply by $5^{2/3}/5^{2/3}$: $x = \frac{16 \cdot 5^{2/3}}{5^{1/3} \cdot 5^{2/3}} = \frac{16 \cdot 5^{2/3}}{5} = \frac{16 \sqrt[3]{25}}{5}$.