Question
Question: A long straight wire (radius = 3.0 mm) carries a constant current distributed uniformly over a cross...
A long straight wire (radius = 3.0 mm) carries a constant current distributed uniformly over a cross section perpendicular to the axis of the wire. If the current density is 100 A/m². The magnitudes of the magnetic field at (a) 2.0 mm from the axis of the wire and (b) 4.0 mm from the axis of the wire is :-
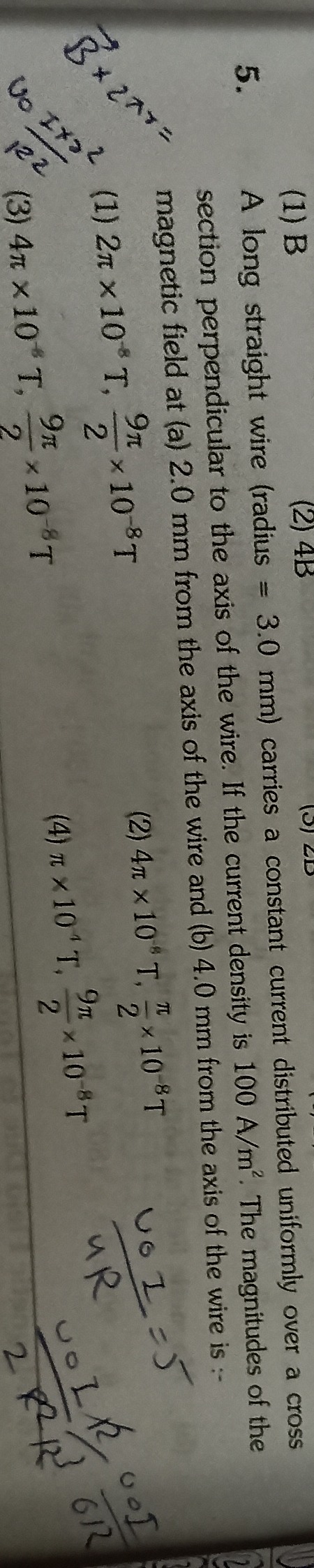
2πx10⁻⁸T, 29πx10⁻⁸T
4π × 10⁻⁸ T, 2πx10⁻⁸T
4π×10⁻⁸T, 29π×10⁻⁸T
π×10⁻⁸ T, 29π×10⁻⁸ T
(3)
Solution
To determine the magnetic field at points inside and outside a long straight wire with a uniform current density, we use Ampere's Law.
Given:
-
Radius of the wire, R=3.0 mm=3.0×10−3 m
-
Current density, J=100 A/m2
-
Permeability of free space, μ0=4π×10−7 T⋅m/A
Formulas for Magnetic Field (B) due to a Long Straight Wire with Uniform Current Density (J):
-
Inside the wire (r<R):
For an Amperian loop of radius r inside the wire, the enclosed current Ienclosed is the current density times the area of the loop:
Ienclosed=J×(πr2)
Applying Ampere's Law (∮B⋅dl=μ0Ienclosed):
Binside(2πr)=μ0(Jπr2)
Binside=2μ0Jr -
Outside the wire (r>R):
For an Amperian loop of radius r outside the wire, the enclosed current Ienclosed is the total current in the wire, Itotal.
Itotal=J×(πR2)
Applying Ampere's Law:
Boutside(2πr)=μ0Itotal
Boutside(2πr)=μ0(JπR2)
Boutside=2rμ0JR2
Calculations:
(a) Magnetic field at ra=2.0 mm from the axis of the wire:
Since ra=2.0 mm<R=3.0 mm, this point is inside the wire.
Using the formula for Binside:
Ba=2μ0Jra
Ba=2(4π×10−7 T⋅m/A)×(100 A/m2)×(2.0×10−3 m)
Ba=24π×10−7×102×2×10−3 T
Ba=4π×10−7×10−1 T
Ba=4π×10−8 T
(b) Magnetic field at rb=4.0 mm from the axis of the wire:
Since rb=4.0 mm>R=3.0 mm, this point is outside the wire.
Using the formula for Boutside:
Bb=2rbμ0JR2
Bb=2×(4.0×10−3 m)(4π×10−7 T⋅m/A)×(100 A/m2)×(3.0×10−3 m)2
Bb=8.0×10−34π×10−7×102×(9.0×10−6) T
Bb=8×10−336π×10−11 T
Bb=836π×10−8 T
Bb=29π×10−8 T
Comparing these results with the given options, we find that:
(a) Ba=4π×10−8 T
(b) Bb=29π×10−8 T
These values match option (3).
The final answer is (3)
Solution Explanation:
The problem requires calculating the magnetic field at two points, one inside and one outside a long straight wire with uniform current density. Ampere's Law is applied for both cases.
-
Inside the wire (r<R): The magnetic field is directly proportional to the distance r from the axis, given by B=2μ0Jr.
-
Outside the wire (r>R): The magnetic field is inversely proportional to the distance r from the axis, and proportional to the square of the wire's radius, given by B=2rμ0JR2.
Substitute the given values for current density, wire radius, and distances to find the magnetic field magnitudes at the specified points.
