Question

$4x^2-3x+2=0$ has two roots $\alpha$ and $\beta$. then find the value of $(2\alpha-3)^2(2\beta-3)^2$

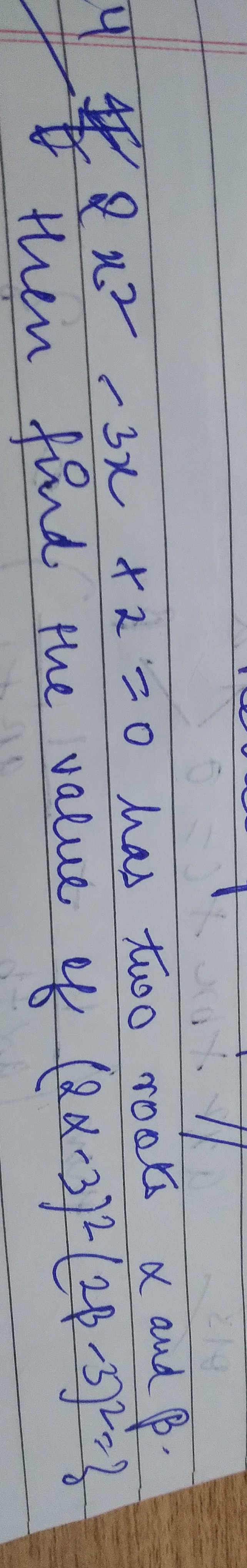
Answer 1

$\frac{169}{4}$

Answer 2

Let $y = 2x-3$. Substituting $x = \frac{y+3}{2}$ into the given equation $4x^2-3x+2=0$ transforms it into a quadratic equation in $y$: $2y^2+9y+13=0$.

The roots of this new equation are $y_1 = 2\alpha-3$ and $y_2 = 2\beta-3$.

The expression to find is $(2\alpha-3)^2(2\beta-3)^2 = y_1^2 y_2^2 = (y_1 y_2)^2$.

For the quadratic equation $2y^2+9y+13=0$, the product of roots $y_1 y_2$ is given by the formula $\frac{c}{a}$, which is $\frac{13}{2}$.

Therefore, the required value is $(y_1 y_2)^2 = \left(\frac{13}{2}\right)^2 = \frac{169}{4}$.