Solveeit Logo
Login

Question

Question: $4x^2-3x+2=0$ has two roots $\alpha$ and $\beta$. then find the value of $(2\alpha-3)^2(2\beta-3)^2$...

4x2−3x+2=04x^2-3x+2=0 has two roots α\alpha and β\beta. then find the value of (2α−3)2(2β−3)2(2\alpha-3)^2(2\beta-3)^2

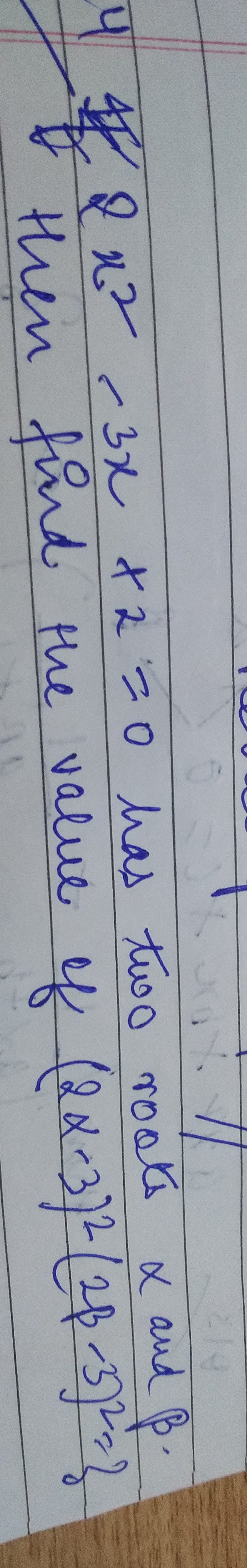
Answer

1694\frac{169}{4}

Explanation

Solution

The given quadratic equation is 4x2−3x+2=04x^2-3x+2=0. By Vieta's formulas, the sum of roots α+β=−−34=34\alpha + \beta = -\frac{-3}{4} = \frac{3}{4} and the product of roots αβ=24=12\alpha \beta = \frac{2}{4} = \frac{1}{2}. The expression to find is (2α−3)2(2β−3)2=[(2α−3)(2β−3)]2(2\alpha-3)^2(2\beta-3)^2 = [(2\alpha-3)(2\beta-3)]^2. Expanding the inner term: (2α−3)(2β−3)=4αβ−6α−6β+9=4αβ−6(α+β)+9(2\alpha-3)(2\beta-3) = 4\alpha\beta - 6\alpha - 6\beta + 9 = 4\alpha\beta - 6(\alpha+\beta) + 9. Substitute the values of α+β\alpha+\beta and αβ\alpha\beta: 4(12)−6(34)+9=2−92+9=11−92=22−92=1324\left(\frac{1}{2}\right) - 6\left(\frac{3}{4}\right) + 9 = 2 - \frac{9}{2} + 9 = 11 - \frac{9}{2} = \frac{22-9}{2} = \frac{13}{2}. Finally, square this result: (132)2=1694\left(\frac{13}{2}\right)^2 = \frac{169}{4}.