Question
Question: $\qquad 4\left[\frac{82\pi}{7}-\frac{18\pi}{7}\right]\left(\cos\frac{3\pi}{7}\right)=?$...
4[782π−718π](cos73π)=?
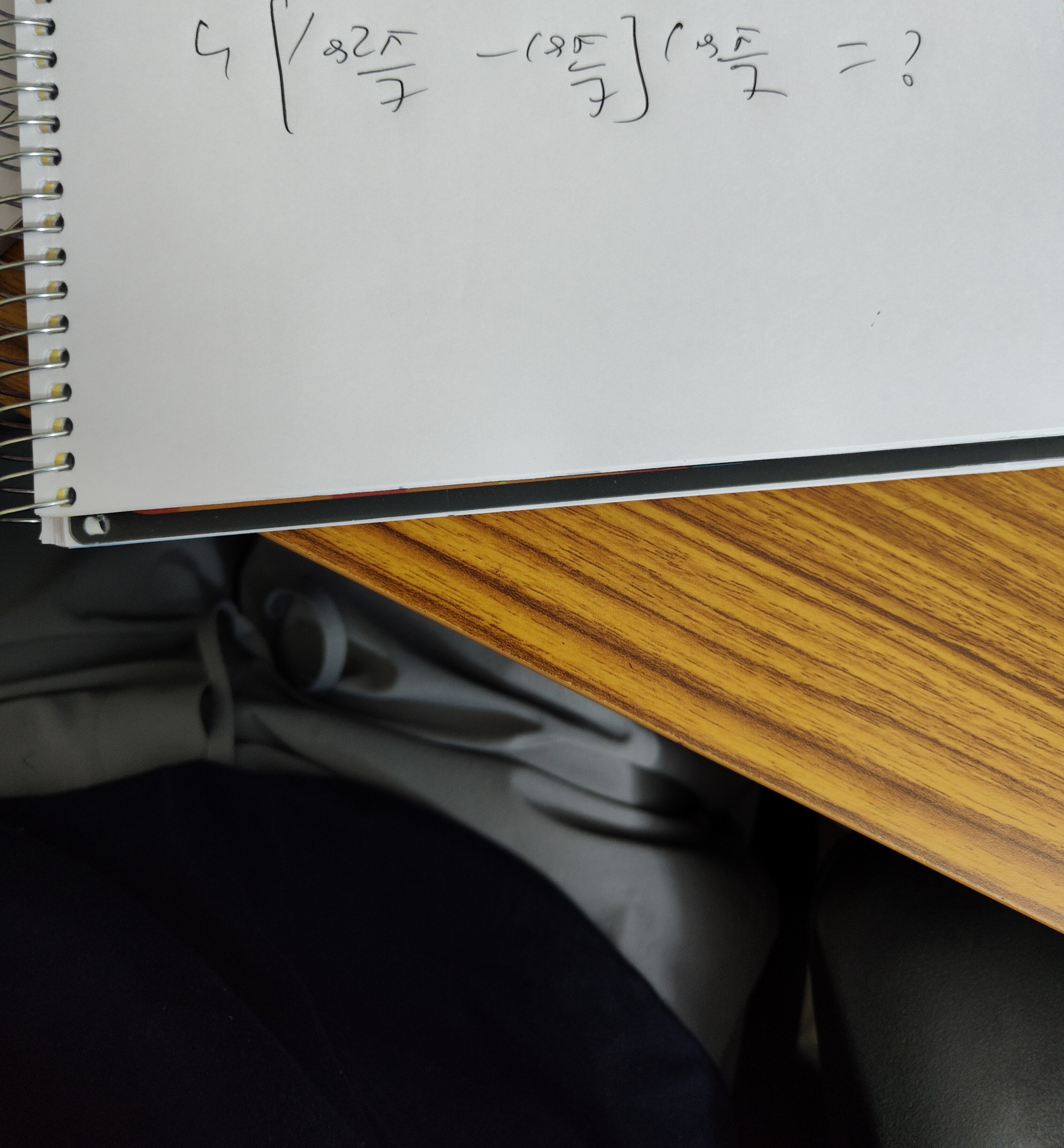
Answer
7256πcos73π
Explanation
Solution
To solve the given expression: 4[782π−718π](cos73π)
First, simplify the terms inside the square brackets: 782π−718π=7(82−18)π=764π
Now, substitute this simplified term back into the expression: 4[764π](cos73π)
Multiply the numerical coefficients: 4×764π=7256π
Finally, multiply by the trigonometric term: 7256πcos73π
The value of cos73π is an irrational number and does not simplify further in a way that would cancel out π or the denominator 7 to yield a simple rational number. Therefore, the expression is simplified to its most compact form.
The final answer is 7256πcos73π.
Explanation of the solution:
- Simplify the bracketed term: Combine the fractions with a common denominator: 782π−718π=7(82−18)π=764π.
- Multiply by the leading constant: Multiply the result from step 1 by 4: 4×764π=7256π.
- Combine with the trigonometric term: Multiply the result from step 2 by cos73π to get the final simplified expression: 7256πcos73π.
