Question

$(4\cot^{2}9^{\circ}-1)(4\cot^{2}27^{\circ}-1)(4\cot^{2}81^{\circ}-1)(4\cot^{2}243^{\circ}-1)$

Answer 1

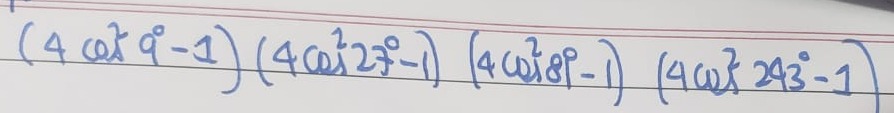
The problem seems to have a typo. Assuming the question is $(4\cos^{2}9^{\circ}-1)(4\cos^{2}27^{\circ}-1)(4\cos^{2}81^{\circ}-1)(4\cos^{2}243^{\circ}-1)$, the answer is 1.

Answer 2

The problem asks for the value of the expression $(4\cot^{2}9^{\circ}-1)(4\cot^{2}27^{\circ}-1)(4\cot^{2}81^{\circ}-1)(4\cot^{2}243^{\circ}-1)$.

Observation and Assumption:

The angles in the product are $9^\circ, 27^\circ, 81^\circ, 243^\circ$, which follow a geometric progression with a common ratio of 3 ($9^\circ, 3 \times 9^\circ, 3^2 \times 9^\circ, 3^3 \times 9^\circ$). This pattern strongly suggests a telescoping product involving a trigonometric identity related to $3\theta$.

A common identity used for such problems is $4\cos^2\theta - 1 = \frac{\sin 3\theta}{\sin \theta}$.

If the terms were of the form $(4\cos^2\theta - 1)$, the problem would be a standard one leading to a simple integer answer.

The presence of $\cot^2\theta$ instead of $\cos^2\theta$ makes the problem significantly more complex and does not typically lead to a simple integer answer using standard identities. Given the context of competitive exams, it is highly probable that there is a typo in the question and that $\cot^2\theta$ should be $\cos^2\theta$. We will proceed with this assumption, as is common practice in such scenarios.

Core Identity:

We use the trigonometric identity: $4\cos^2\theta - 1 = \frac{\sin 3\theta}{\sin \theta}$

Proof of the Identity:

We know the triple angle formula for sine: $\sin 3\theta = 3\sin\theta - 4\sin^3\theta$. Dividing both sides by $\sin\theta$ (assuming $\sin\theta \neq 0$): $\frac{\sin 3\theta}{\sin \theta} = \frac{3\sin\theta - 4\sin^3\theta}{\sin\theta} = 3 - 4\sin^2\theta$ Using the Pythagorean identity $\sin^2\theta = 1 - \cos^2\theta$: $3 - 4(1 - \cos^2\theta) = 3 - 4 + 4\cos^2\theta = 4\cos^2\theta - 1$ Thus, the identity $4\cos^2\theta - 1 = \frac{\sin 3\theta}{\sin \theta}$ is verified.

Applying the Identity to Each Term:

Now, we apply this identity to each term in the product, assuming the corrected form $(4\cos^2\theta - 1)$:

1. For $\theta = 9^\circ$: $4\cos^2 9^\circ - 1 = \frac{\sin(3 \times 9^\circ)}{\sin 9^\circ} = \frac{\sin 27^\circ}{\sin 9^\circ}$

2. For $\theta = 27^\circ$: $4\cos^2 27^\circ - 1 = \frac{\sin(3 \times 27^\circ)}{\sin 27^\circ} = \frac{\sin 81^\circ}{\sin 27^\circ}$

3. For $\theta = 81^\circ$: $4\cos^2 81^\circ - 1 = \frac{\sin(3 \times 81^\circ)}{\sin 81^\circ} = \frac{\sin 243^\circ}{\sin 81^\circ}$

4. For $\theta = 243^\circ$: $4\cos^2 243^\circ - 1 = \frac{\sin(3 \times 243^\circ)}{\sin 243^\circ} = \frac{\sin 729^\circ}{\sin 243^\circ}$

Multiplying the Terms (Telescoping Product):

Let P be the product of these terms: $P = \left(\frac{\sin 27^\circ}{\sin 9^\circ}\right) \times \left(\frac{\sin 81^\circ}{\sin 27^\circ}\right) \times \left(\frac{\sin 243^\circ}{\sin 81^\circ}\right) \times \left(\frac{\sin 729^\circ}{\sin 243^\circ}\right)$ This is a telescoping product, where the numerator of each term cancels with the denominator of the subsequent term: $P = \frac{\sin 729^\circ}{\sin 9^\circ}$

Simplifying the Result:

We need to simplify $\sin 729^\circ$. We know that $\sin(n \cdot 360^\circ + \theta) = \sin\theta$ for any integer $n$. We can write $729^\circ$ as $2 \times 360^\circ + 9^\circ = 720^\circ + 9^\circ$. So, $\sin 729^\circ = \sin(720^\circ + 9^\circ) = \sin 9^\circ$.

Substituting this back into the expression for P: $P = \frac{\sin 9^\circ}{\sin 9^\circ} = 1$

The final answer is 1.