Question

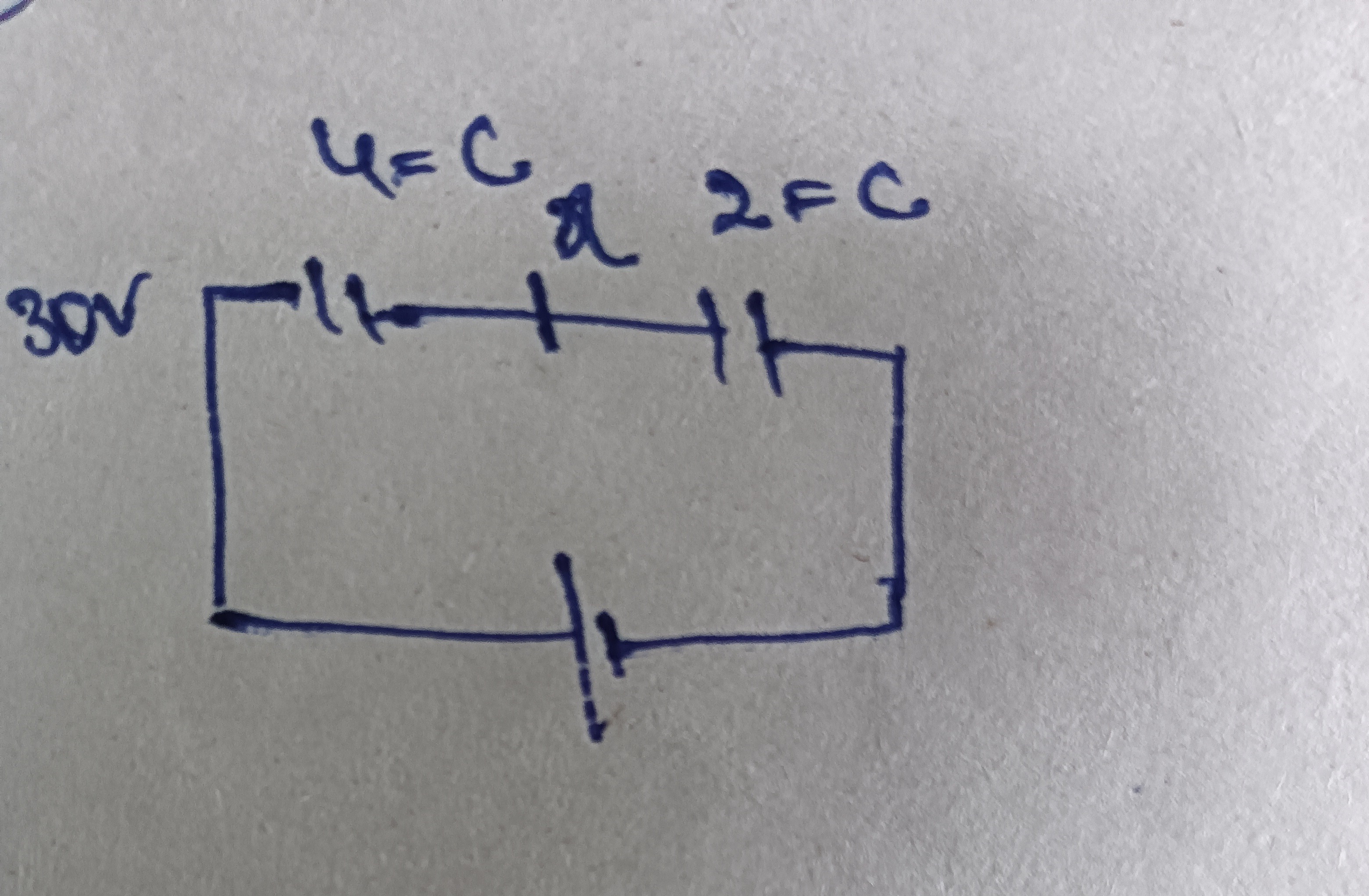
In the given circuit, two capacitors with capacitances $C_1 = 4$ F and $C_2 = 2$ F are connected in series to a voltage source of $V = 30$ V. Determine the charge on each capacitor.

• A. The charge on each capacitor is 20 C.
• B. The charge on the 4 F capacitor is 60 C and on the 2 F capacitor is 30 C.
• C. The charge on each capacitor is 40 C.
• D. The charge on the 4 F capacitor is 30 C and on the 2 F capacitor is 60 C.

Answer 1

Answer: (C)

The charge on each capacitor is 40 C.

Answer 2

The capacitors $C_1 = 4$ F and $C_2 = 2$ F are connected in series to a voltage source $V = 30$ V.

First, we calculate the equivalent capacitance ($C_{eq}$) for capacitors in series: $\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2}$ $\frac{1}{C_{eq}} = \frac{1}{4 \text{ F}} + \frac{1}{2 \text{ F}} = \frac{1+2}{4} = \frac{3}{4} \text{ F}^{-1}$ $C_{eq} = \frac{4}{3} \text{ F}$

Next, we calculate the total charge ($Q$) stored in the equivalent capacitor using the formula $Q = C_{eq}V$: $Q = \left(\frac{4}{3} \text{ F}\right) \times (30 \text{ V}) = 40 \text{ C}$

For capacitors connected in series, the charge on each capacitor is the same as the total charge stored by the combination. Therefore, the charge on the first capacitor ($Q_1$) is 40 C, and the charge on the second capacitor ($Q_2$) is also 40 C. $Q_1 = Q_2 = Q = 40 \text{ C}$