Question

4a cosec a.

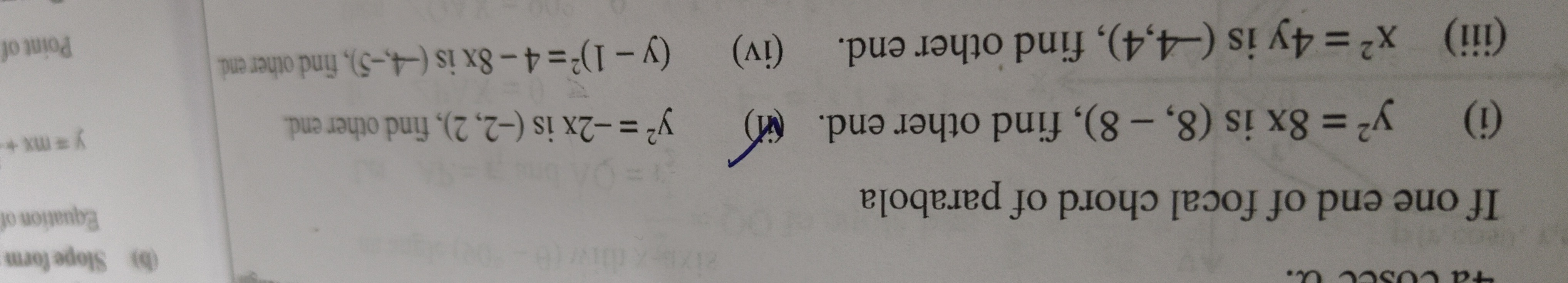
• A. If one end of focal chord of parabola $y^2 = 8x$ is $(8,8)$, find other end.
• B. If one end of focal chord of parabola $y^2 = -2x$ is $(-2, 2)$, find other end.
• C. If one end of focal chord of parabola $x^2 = 4y$ is $(-4,4)$, find other end.
• D. If one end of focal chord of parabola $(y - 1)^2 = 4-8x$ is $(-4,-5)$, find other end.

Answer 1

The question is a multipart question. Please refer to the detailed breakdown for each part.

Answer 2

The problem asks to find the other end of a focal chord for four different parabolas, given one endpoint of the chord. The general approach involves identifying the type of parabola, its focus, and applying specific properties of focal chords.

For parabolas of the form $y^2 = 4ax$, the focus is at $(a, 0)$ and if $(x_1, y_1)$ and $(x_2, y_2)$ are the endpoints of a focal chord, then $x_1 x_2 = a^2$. Alternatively, using the parametric form $(at^2, 2at)$, the condition for a focal chord is $t_1 t_2 = -1$.

For parabolas of the form $x^2 = 4ay$, the focus is at $(0, a)$ and if $(x_1, y_1)$ and $(x_2, y_2)$ are the endpoints of a focal chord, then $y_1 y_2 = a^2$. The parametric form is $(2at, at^2)$, and the condition for a focal chord remains $t_1 t_2 = -1$.

For translated parabolas, the coordinate system can be shifted, or the general parametric form for translated parabolas can be used.

Detailed breakdown for each part:

(i) Parabola $y^2 = 8x$, one end is $(8,8)$.

• Equation: $y^2 = 8x \implies y^2 = 4(2)x$. So, $a=2$.
• Given end $(x_1, y_1) = (8,8)$.
• Using $x_1 x_2 = a^2$: $8 \cdot x_2 = 2^2 \implies 8x_2 = 4 \implies x_2 = \frac{1}{2}$.
• The point $(x_2, y_2)$ lies on the parabola: $y_2^2 = 8x_2 = 8(\frac{1}{2}) = 4 \implies y_2 = \pm 2$.
• Using parametric form: $a=2$, points are $(2t^2, 4t)$. For $(8,8)$, $4t_1=8 \implies t_1=2$.
• For a focal chord, $t_1 t_2 = -1 \implies 2t_2 = -1 \implies t_2 = -\frac{1}{2}$.
• Other end: $(2t_2^2, 4t_2) = (2(-\frac{1}{2})^2, 4(-\frac{1}{2})) = (2(\frac{1}{4}), -2) = (\frac{1}{2}, -2)$.

(ii) Parabola $y^2 = -2x$, one end is $(-2, 2)$.

• Equation: $y^2 = -2x \implies y^2 = 4(-\frac{1}{2})x$. So, $a=-\frac{1}{2}$.
• Given end $(x_1, y_1) = (-2, 2)$.
• Using $x_1 x_2 = a^2$: $(-2) \cdot x_2 = (-\frac{1}{2})^2 \implies -2x_2 = \frac{1}{4} \implies x_2 = -\frac{1}{8}$.
• The point $(x_2, y_2)$ lies on the parabola: $y_2^2 = -2x_2 = -2(-\frac{1}{8}) = \frac{1}{4} \implies y_2 = \pm \frac{1}{2}$.
• Using parametric form: $a=-\frac{1}{2}$, points are $(-\frac{1}{2}t^2, -t)$. For $(-2,2)$, $-t_1=2 \implies t_1=-2$.
• For a focal chord, $t_1 t_2 = -1 \implies -2t_2 = -1 \implies t_2 = \frac{1}{2}$.
• Other end: $(-\frac{1}{2}t_2^2, -t_2) = (-\frac{1}{2}(\frac{1}{2})^2, -\frac{1}{2}) = (-\frac{1}{2}(\frac{1}{4}), -\frac{1}{2}) = (-\frac{1}{8}, -\frac{1}{2})$.

(iii) Parabola $x^2 = 4y$, one end is $(-4,4)$.

• Equation: $x^2 = 4y \implies x^2 = 4(1)y$. So, $a=1$.
• Given end $(x_1, y_1) = (-4, 4)$.
• Using $y_1 y_2 = a^2$: $4 \cdot y_2 = 1^2 \implies 4y_2 = 1 \implies y_2 = \frac{1}{4}$.
• The point $(x_2, y_2)$ lies on the parabola: $x_2^2 = 4y_2 = 4(\frac{1}{4}) = 1 \implies x_2 = \pm 1$.
• Using parametric form: $a=1$, points are $(2t, t^2)$. For $(-4,4)$, $2t_1=-4 \implies t_1=-2$.
• For a focal chord, $t_1 t_2 = -1 \implies -2t_2 = -1 \implies t_2 = \frac{1}{2}$.
• Other end: $(2t_2, t_2^2) = (2(\frac{1}{2}), (\frac{1}{2})^2) = (1, \frac{1}{4})$.

(iv) Parabola $(y - 1)^2 = 4-8x$, one end is $(-4,-5)$.

• Equation: $(y - 1)^2 = -8(x - \frac{1}{2})$. This is a translated parabola $(y-k)^2 = 4a(x-h)$ with $h=\frac{1}{2}$, $k=1$, and $4a=-8 \implies a=-2$.
• The parametric form for this translated parabola is $(h + at^2, k + 2at) = (\frac{1}{2} - 2t^2, 1 - 4t)$.
• Given end $(x_1, y_1) = (-4, -5)$.
• Equating with parametric form:
  • $y_1 = 1 - 4t_1 = -5 \implies -4t_1 = -6 \implies t_1 = \frac{3}{2}$.
  • Check with x-coordinate: $x_1 = \frac{1}{2} - 2t_1^2 = \frac{1}{2} - 2(\frac{3}{2})^2 = \frac{1}{2} - 2(\frac{9}{4}) = \frac{1}{2} - \frac{9}{2} = -\frac{8}{2} = -4$. This matches.
• For a focal chord, $t_1 t_2 = -1 \implies \frac{3}{2} t_2 = -1 \implies t_2 = -\frac{2}{3}$.
• Other end: $(\frac{1}{2} - 2t_2^2, 1 - 4t_2) = (\frac{1}{2} - 2(-\frac{2}{3})^2, 1 - 4(-\frac{2}{3})) = (\frac{1}{2} - 2(\frac{4}{9}), 1 + \frac{8}{3}) = (\frac{1}{2} - \frac{8}{9}, \frac{3+8}{3}) = (\frac{9-16}{18}, \frac{11}{3}) = (-\frac{7}{18}, \frac{11}{3})$.