Question

Let

$A = \begin{bmatrix} 0 & 1 & 2 \\ x & 0 & 3 \\ 1 & y & 0 \end{bmatrix}$, where x,y ∈ R. If $A^3 = A$ and the positive value of x belongs to the interval (n - 1, n] where $n \in N$, then $\frac{45}{n^3}$ is equal to

Answer 1

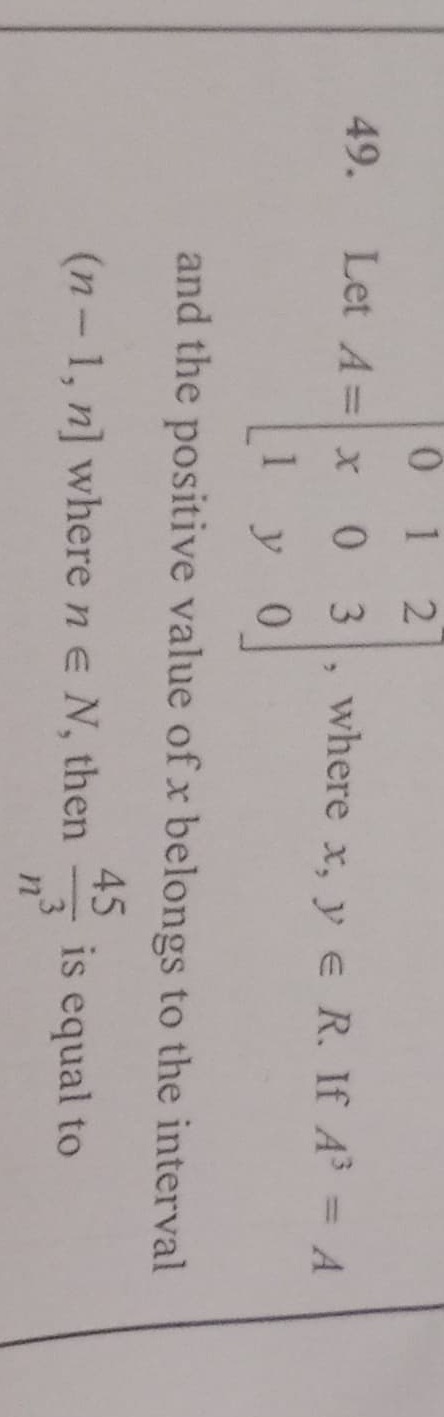
45/8

Answer 2

To solve the problem, we are given the matrix $A = \begin{bmatrix} 0 & 1 & 2 \\ x & 0 & 3 \\ 1 & y & 0 \end{bmatrix}$ and the condition $A^3 = A$. We need to find the positive value of $x$, determine $n$ such that $x \in (n-1, n]$, and then calculate $\frac{45}{n^3}$.

First, let's calculate $A^2$: $A^2 = A \cdot A = \begin{bmatrix} 0 & 1 & 2 \\ x & 0 & 3 \\ 1 & y & 0 \end{bmatrix} \begin{bmatrix} 0 & 1 & 2 \\ x & 0 & 3 \\ 1 & y & 0 \end{bmatrix} = \begin{bmatrix} (0)(0)+(1)(x)+(2)(1) & (0)(1)+(1)(0)+(2)(y) & (0)(2)+(1)(3)+(2)(0) \\ (x)(0)+(0)(x)+(3)(1) & (x)(1)+(0)(0)+(3)(y) & (x)(2)+(0)(3)+(3)(0) \\ (1)(0)+(y)(x)+(0)(1) & (1)(1)+(y)(0)+(0)(y) & (1)(2)+(y)(3)+(0)(0) \end{bmatrix}$ $A^2 = \begin{bmatrix} x+2 & 2y & 3 \\ 3 & x+3y & 2x \\ xy & 1 & 2+3y \end{bmatrix}$

Next, let's calculate $A^3 = A^2 \cdot A$: $A^3 = \begin{bmatrix} x+2 & 2y & 3 \\ 3 & x+3y & 2x \\ xy & 1 & 2+3y \end{bmatrix} \begin{bmatrix} 0 & 1 & 2 \\ x & 0 & 3 \\ 1 & y & 0 \end{bmatrix} = \begin{bmatrix} (x+2)(0)+(2y)(x)+(3)(1) & (x+2)(1)+(2y)(0)+(3)(y) & (x+2)(2)+(2y)(3)+(3)(0) \\ (3)(0)+(x+3y)(x)+(2x)(1) & (3)(1)+(x+3y)(0)+(2x)(y) & (3)(2)+(x+3y)(3)+(2x)(0) \\ (xy)(0)+(1)(x)+(2+3y)(1) & (xy)(1)+(1)(0)+(2+3y)(y) & (xy)(2)+(1)(3)+(2+3y)(0) \end{bmatrix}$ $A^3 = \begin{bmatrix} 2xy+3 & x+2+3y & 2x+4+6y \\ x^2+3xy+2x & 3+2xy & 6+3x+9y \\ x+2+3y & xy+2y+3y^2 & 2xy+3 \end{bmatrix}$

Now, we equate $A^3 = A$: $\begin{bmatrix} 2xy+3 & x+2+3y & 2x+4+6y \\ x^2+3xy+2x & 3+2xy & 6+3x+9y \\ x+2+3y & xy+2y+3y^2 & 2xy+3 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 2 \\ x & 0 & 3 \\ 1 & y & 0 \end{bmatrix}$

Equating the corresponding elements, we get a system of equations:

1. From $a_{11}$: $2xy+3 = 0 \implies 2xy = -3$
2. From $a_{12}$: $x+2+3y = 1 \implies x+3y = -1$
3. From $a_{13}$: $2x+4+6y = 2 \implies 2(x+3y)+4 = 2$. Substituting $x+3y=-1$ from (2), we get $2(-1)+4=2 \implies -2+4=2 \implies 2=2$. This is consistent.
4. From $a_{21}$: $x^2+3xy+2x = x \implies x^2+3xy+x = 0$.
5. From $a_{22}$: $3+2xy = 0$. This is the same as (1).
6. From $a_{23}$: $6+3x+9y = 3 \implies 3(2+x+3y) = 3 \implies 2+x+3y = 1 \implies x+3y = -1$. This is the same as (2).
7. From $a_{31}$: $x+2+3y = 1$. This is the same as (2).
8. From $a_{32}$: $xy+2y+3y^2 = y \implies xy+y+3y^2 = 0 \implies y(x+1+3y) = 0$. Since $2xy=-3$, $y \neq 0$. Therefore, $x+1+3y = 0 \implies x+3y = -1$. This is the same as (2).
9. From $a_{33}$: $2xy+3 = 0$. This is the same as (1).

So, we have two independent equations: (I) $2xy = -3$ (II) $x+3y = -1$

From equation (II), we can express $y$ in terms of $x$: $3y = -1-x \implies y = \frac{-1-x}{3}$. Substitute this expression for $y$ into equation (I): $2x \left( \frac{-1-x}{3} \right) = -3$ $2x(-1-x) = -9$ $-2x - 2x^2 = -9$ $2x^2 + 2x - 9 = 0$

This is a quadratic equation for $x$. We use the quadratic formula $x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$: $x = \frac{-2 \pm \sqrt{2^2 - 4(2)(-9)}}{2(2)}$ $x = \frac{-2 \pm \sqrt{4 + 72}}{4}$ $x = \frac{-2 \pm \sqrt{76}}{4}$ $x = \frac{-2 \pm 2\sqrt{19}}{4}$ $x = \frac{-1 \pm \sqrt{19}}{2}$

We are given that $x$ is a positive value. Therefore, we choose the positive root: $x = \frac{-1 + \sqrt{19}}{2}$

Now, we need to find $n \in N$ such that $x \in (n-1, n]$. We know that $4^2 = 16$ and $5^2 = 25$, so $4 < \sqrt{19} < 5$. To get a more precise estimate, $4.3^2 = 18.49$ and $4.4^2 = 19.36$. So $4.3 < \sqrt{19} < 4.4$. Let's use these bounds to estimate $x$: Lower bound for $x$: $\frac{-1 + 4.3}{2} = \frac{3.3}{2} = 1.65$ Upper bound for $x$: $\frac{-1 + 4.4}{2} = \frac{3.4}{2} = 1.7$ So, $1.65 < x < 1.7$.

This implies that $x$ lies between 1 and 2. Therefore, $x \in (1, 2]$. Comparing this with the given interval $(n-1, n]$, we find that $n-1 = 1$ and $n=2$. Thus, $n=2$.

Finally, we need to calculate $\frac{45}{n^3}$: $\frac{45}{n^3} = \frac{45}{2^3} = \frac{45}{8}$.

The final answer is $\boxed{\frac{45}{8}}$.