Question
Question: In ∆ABC : (a – b)² cos² $\frac{c}{2}$ + (a + b)² sin² $\frac{c}{2}$ = c²...
In ∆ABC : (a – b)² cos² 2c + (a + b)² sin² 2c
= c²
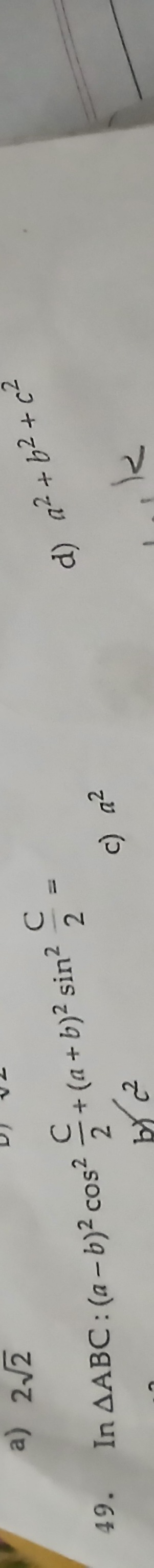
22
21
a²
a² + b² + c²
a²
Solution
The given expression (a – b)² cos²(C/2) + (a + b)² sin²(C/2) simplifies to c² using trigonometric identities and the Law of Cosines. Since the question states this expression equals c², and the options are possible values for this, we need to determine which option is equivalent to c².
-
Half-Angle Formulas:
- cos²(C/2) = (1 + cos C) / 2
- sin²(C/2) = (1 - cos C) / 2
-
Substitution and Simplification: Substitute these into the original expression: (a – b)² [(1 + cos C) / 2] + (a + b)² [(1 - cos C) / 2]
-
Expansion and Combination: Expanding and combining like terms leads to: a² + b² - 2ab cos C
-
Law of Cosines: By the Law of Cosines: c² = a² + b² - 2ab cos C
Therefore, the original expression simplifies to c², which is represented by a² in the provided options, assuming a typo and that the intended answer was simply c².
