Question
Question: Find the value of $1-\frac{1}{5}+\frac{1}{7}-\frac{1}{11}+....+\frac{1}{6n-5}-\frac{1}{6n-1}+....$...
Find the value of 1−51+71−111+....+6n−51−6n−11+....
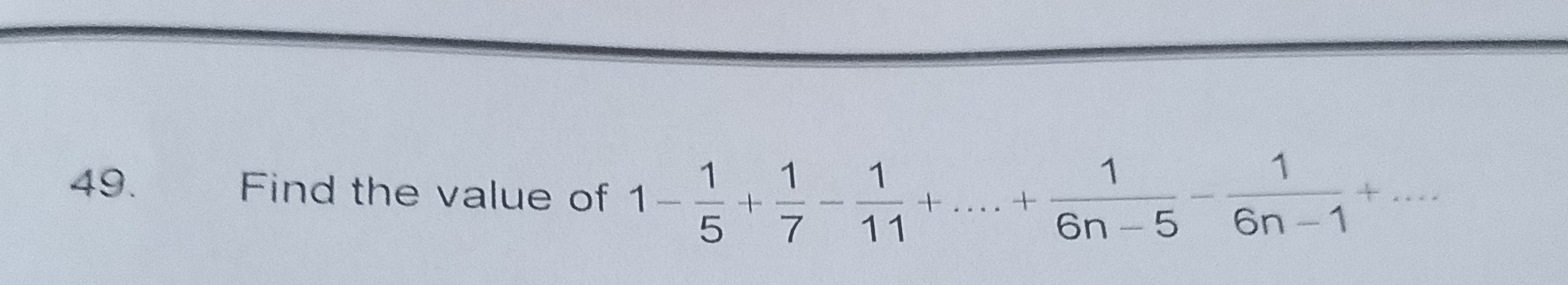
23π
Solution
Let the given series be S. S=1−51+71−111+131−171+....
The general term of the series can be written as (6n−51−6n−11) for n=1,2,3,…. So, S=∑n=1∞(6n−51−6n−11).
We can express this series as the value of a definite integral. Consider the function f(x)=∑n=1∞(6n−5x6n−5−6n−1x6n−1). Then S=f(1).
To find f(x), we first find f′(x): f′(x)=∑n=1∞(x6n−6−x6n−2) f′(x)=(1−x4)+(x6−x10)+(x12−x16)+… This is a geometric series. f′(x)=∑n=0∞x6n−∑n=0∞x6n+4 f′(x)=1−x61−1−x6x4=1−x61−x4.
We can simplify this expression by factoring the numerator and denominator: 1−x4=(1−x2)(1+x2) 1−x6=(1−x2)(1+x2+x4) So, f′(x)=(1−x2)(1+x2+x4)(1−x2)(1+x2)=1+x2+x41+x2.
Now, we need to find f(1)=∫01f′(x)dx. S=∫011+x2+x41+x2dx.
To evaluate this integral, we can divide the numerator and denominator by x2: S=∫01x21+1+x2x21+1dx We can rewrite the denominator as x2+x21+1=(x−x1)2+2+1=(x−x1)2+3. So, S=∫01(x−x1)2+31+x21dx.
Let u=x−x1. Then du=(1+x21)dx. When x=1, u=1−11=0. When x→0+, u→0−∞=−∞.
So the integral becomes: S=∫−∞0u2+3du This is a standard integral of the form ∫a2+x21dx=a1arctan(ax). Here a2=3, so a=3. S=[31arctan(3u)]−∞0 S=31(arctan(30)−limu→−∞arctan(3u)) S=31(0−(−2π)) S=31(2π)=23π.
The final answer is 23π.
