Question

$3tan \frac{6\pi}{18}-27tan \frac{4\pi}{18}+33 tan^2 \frac{2\pi}{18}$ is equal to

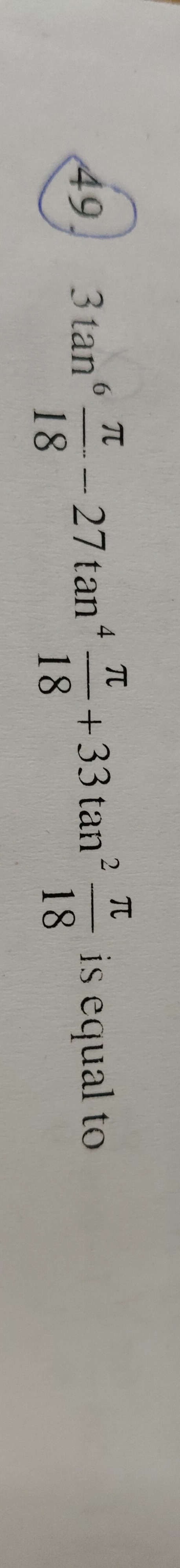
Answer 1

1

Answer 2

Let $x = \tan \frac{\pi}{18}$. The expression to be evaluated is $3x^6 - 27x^4 + 33x^2$.

Let $\theta = \frac{\pi}{18}$. Then $3\theta = \frac{3\pi}{18} = \frac{\pi}{6}$.

The triple angle formula for tangent is $\tan(3\theta) = \frac{3\tan\theta - \tan^3\theta}{1 - 3\tan^2\theta}$.

Substitute $\tan(3\theta) = \tan \frac{\pi}{6} = \frac{1}{\sqrt{3}}$ and $\tan\theta = x$:

$\frac{1}{\sqrt{3}} = \frac{3x - x^3}{1 - 3x^2}$

$1 - 3x^2 = \sqrt{3}(3x - x^3)$

Square both sides:

$(1 - 3x^2)^2 = 3(3x - x^3)^2$

$1 - 6x^2 + 9x^4 = 3(9x^2 - 6x^4 + x^6)$

$1 - 6x^2 + 9x^4 = 27x^2 - 18x^4 + 3x^6$

Rearrange the terms:

$3x^6 - 18x^4 - 9x^4 + 27x^2 + 6x^2 - 1 = 0$

$3x^6 - 27x^4 + 33x^2 - 1 = 0$

Thus, $3x^6 - 27x^4 + 33x^2 = 1$.