Question

Solve the system of equations: $48x - 64y = 48y + 24$ $ry = \frac{1}{8} - 12x$

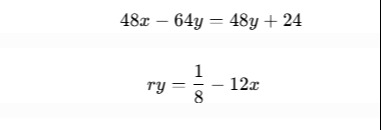
Answer 1

$x = \frac{7 + 12r}{24\,(r + 28)},\quad y = -\,\frac{329}{56\,(r + 28)},\quad r \neq -28$

Answer 2

Step 1. Rearrange the first equation:

$$48x - 64y = 48y + 24 \;\Longrightarrow\; 48x = 112y + 24 \;\Longrightarrow\; y = \frac{48x - 24}{112} = \frac{6x - 3}{14}\,.$$

Step 2. Substitute $y$ into the second equation $ry = \tfrac{1}{8} - 12x$:

$$r\!\Bigl(\frac{6x - 3}{14}\Bigr) = \frac{1}{8} - 12x \;\Longrightarrow\; r(6x - 3) = 14\Bigl(\frac{1}{8} - 12x\Bigr) = \frac{7}{4} - 168x.$$

Rearrange for $x$:

$$6r\,x + 168x = \frac{7}{4} + 3r \;\Longrightarrow\; x\,(6r + 168) = \frac{7}{4} + 3r \;\Longrightarrow\; x = \frac{\frac{7}{4} + 3r}{6(r + 28)} = \frac{7 + 12r}{24\,(r + 28)}\,.$$

Step 3. Plug $x$ back into $y = \frac{6x - 3}{14}$:

$$y = \frac{6\Bigl(\frac{7 + 12r}{24(r + 28)}\Bigr) - 3}{14} = \frac{\frac{7 + 12r}{4(r + 28)} - 3}{14} = \frac{(7 + 12r) - 12(r + 28)}{56(r + 28)} = -\,\frac{329}{56\,(r + 28)}\,.$$

Conclusion:

$$x = \frac{7 + 12r}{24(r + 28)},\quad y = -\frac{329}{56(r + 28)},\quad r \neq -28.$$